Le problème que nous allons traiter ici n’est autre que celui de l’infini physique. L’univers est-il infini ? Est-il possible de marcher droit devant soi sans jamais être arrêté ? Ce problème se trouve étroitement lié à celui de la structure géométrique de l’univers : la somme des angles d’un triangle physique est-elle égale à deux droits ? Il se trouve également lié au problème du passé et de l’avenir de l’univers : les propriétés métriques de l’univers ont-elles toujours été ce qu’elles sont maintenant et ne doivent-elles pas se modifier dans l’avenir ?
Tout cela peut paraître un peu étrange et incompréhensible pour un être humain, il est commun de dire en effet que la notion d’infini échappe à notre compréhension. Il n’en est que plus curieux de voir comment l’expérience permet d’aborder ce sujet et quelles perspectives nouvelles s’ouvrent devant nous.
La notion d’inifini en mathématiques
L’idée de l’infini en arithmétique se réduit à ceci : après tout nombre entier il y en a un autre. Henri Poincaré a dit que l’introduction de l’infini en arithmétique avait coïncidé avec l’introduction en logique d’un raisonnement d’une nature spéciale dit : raisonnement par récurrence. Voici en quoi consiste ce raisonnement : nous voulons démontrer que telle propriété est vraie pour tous les nombres, nous établissons pour cela que, si la propriété est vraie pour un nombre n, elle est vraie pour le nombre n+1, puis l’ayant établie pour le nomhre 1 nous estimons par là même I’avoir établie pour tous les nombres. Le raisonnement par récurrence, on le voit, est étroitement lié à la notion d’infini arithmétique, et notre esprit s’accommode fort bien d’un raisonnement, de cette nature. Nous concevons en effet cette notion d’infini arithmétique parce que nous l’avons reliée à des notions de nombres finis : étant donné un nombre quelconque, nous savons l’atteindre par l’addition d’un nombre suffisant d’unités et nous concevons qu’une telle opération, limitée en pratique, puisse ne pas l’être
a priori
, en sorte que nous pouvons ne pas fixer de limite aux nombres sur lesquels nous raisonnons.

Cette notion d’infini étant bien examinée, on se rend compte que le mot infini n’est qu’un vocable destiné à abréger le langage et à permettre d’exprimer un raisonnement d’une manière plus courte.
Lorsque nous disons qu’un nombre variable tend vers l’infini, nous voulons simplement dire par là qu’étant donnée une grandeur quelconque, il arrivera un moment où le nombre considéré dépassera cette grandeur ; pour définir un nombre qui tend vers l’infini, nous ne faisons donc appel qu’à des éléments finis parfaitement concevables et l’expression « tendre vers l’infini » et, le mot « infini » lui-même ne sont que des abréviations pour exprimer une pensée précise et parfaitement concevable.
On ne saurait trop s’élever contre l’affirmation gratuite que l’infini échappe à notre compréhension et peut nous épouvanter. Cette notion ne peut nous échapper que si nous perdons de vue sa définition et son sens véritable.
De même qu’en arithmétique le mot infini a un sens bien déterminé, en géométrie l’idée qu’une droite est infinie se réduit en définitive à ce fait que, sur cette droite, si l’on compte les distances des points à partir d’une certaine origine, après tout mètre ou après tout kilomètre il y en a un autre. La notion d’infini en géométrie se réduit donc à la constatation expérimentale que si nous marchons toujours dans le même sens sur une droite infinie nous ne serons jamais arrêtés. La notion d’infini géométrique n’est pas plus obscure ni plus mystérieuse que celle du rapport de deux longueurs sur une droite. La preuve en est que nous concevrions difficilement une droite qui ne serait pas infinie.
Il importerait de dire un mot d’autres infinis qui se sont introduits en mathématiques il y a une quarantaine d’années : les infinis non dénombrables. Mais si, du point de vue du raisonnement mathématique, ils ont le même caractère d’abstraction que l’infini arithmétique ou l’infini sur une droite, c’est-à-dire de n’être que des abréviations de langage ils n’ont pas la même signification ni le même intérêt physique.
Géométrie et édifice logique
Il importe, avant d’aller plus loin, de dire que nous entendons par géométrie une science expérimentale : la science de la mesure des longueurs et des angles dans l’univers qui nous entoure, ou, si l’on préfère, et bien que le terme soit impropre, une géodésie de l’univers. La géométrie apparaît donc, d’après notre définition, comme étant un chapitre de la physique. Nous admettons pour cela que certains corps ont des dimensions constantes et qu’au moyen de ces corps nous pouvons mesurer l’univers et en faire expérimentalement la géométrie.
Notre définition de la géométrie peut paraître étrange et peu conforme aux méthodes employées dans les cours classiques de mathématiques, aussi pour la clarté du langage désignerons-nous du terme « d’édifice logique » le corps de doctrine que l’on enseigne d’ordinaire sous le nom de géométrie : on raisonne sur des droites, sur des distances, sur des angles, etc... sans faire d’expériences, et l’on constitue une science qui n’est au fond qu’un chapitre de la logique et qui consiste principalement à déduire de certains postulats de départ des propriétés qui en découlent logiquement. Expérimentalement « l’édifice logique » n’est ni vrai ni faux, il ne constitue qu’une tautologie.
L’édifice logique le plus connu (c’est même le seul qui le soit du vulgaire) est l’édifice euclidien appelé communément géométrie euclidienne.
Les lois de la géométrie euclidienne sont bien connues de tous, car cette géométrie est devenue intuitive pour l’homme et se trouve enseignée d’une manière classique. Par exemple dans cette géométrie, la distance entre deux points A et B est égale à la somme des distances AC et CB si le point C se trouve entre A et B. Dans cette géométrie et c’est là un de ses postulats les plus connus, la somme des angles d’un triangle est égale à deux droits. On sait déduire de ces postulats les relations qui lient les côtés et les angles d’un triangle, et d’une façon plus générale, les longueurs d’une figure géométrique quelconque. La géométrie analytique classique est la partie la plus parfaite de l’édifice logique euclidien.
On appelle espace euclidien un continuum à trois dimensions ( [1].) dans lequel les longueurs et les angles sont régis par les lois de la géométrie euclidienne.
Une des propriétés qui nous intéresse le plus aujourd’hui est la suivante : l’espace euclidien est infini dans toutes les directions. Ceci veut dire que, sur une droite quelconque, on peut ajouter des mètres les uns au bout des autres sans jamais être arrêté ni, nous verrons plus loin le sens de cette affirmation, revenir à son point de départ en faisant le tour de l’espace.
La notion ancienne de l’espace physique
On a cru jusqu’en 1916 que l’espace dans lequel nous vivions était euclidien, c’est-à-dire que la géométrie, science physique de la mesure des longueurs, coïncidait rigoureusement avec l’édifice logique euclidien et, de fait, cela est vrai à un très haut degré d’approximation. Lorsque nous traçons un triangle sur le papier la somme de ses angles est égale à deux droits. Si l’on veut faire appel à des expériences précises, les mesures astronomiques des angles que font entre eux les rayons lumineux qui parviennent à divers observateurs donnent des résultats en accord avec la géométrie euclidienne, comme si ces rayons étaient des lignes droites et comme si l’espace dans lequel nous vivons était euclidien. Un autre point qui nous intéresse également est cette constatation qu’aussi loin que porte notre regard nous ne voyons pas de limite ni, que l’on excuse cette anticipation, de retour de l’espace sur lui-même.
Cette constatation du fait que l’espace est euclidien est si fréquente qu’elle fait partie de notre expérience journalière ; elle s’est implantée dans l’esprit humain au cours des siècles et paraît être maintenant une idée innée. L’homme a pris l’habitude de considérer l’espace comme étant euclidien, et il a fini par penser qu’il ne pouvait être autrement et que l’idée d’espace euclidien était dans son esprit avant d’être dans la nature.
On peut dire que l’espace euclidien est une notion atavique à ce point qu’il devient très difficile même au savant de penser un espace non euclidien. On peut dire aussi que cette opinion que l’espace physique est euclidien est une constatation expérimentale élémentaire.
L’univers galiléen
Pour être complet il importe d’introduire en physique une autre donnée qui est le temps.
Le temps est une variable qui jointe à l’espace permet de localiser les événements. Lorsque nous pouvons fixer en quel point de l’espace et à quelle époque se produit un événement quelconque, nous avons la possibilité de définir sans ambiguïté tous les phénomènes constatables expérimentalement par nous. La notion commune de temps est celle de temps absolu.
Avec ces notions d’espace et de temps absolus, l’homme a pu pendant trois siècles constituer la physique. La mécanique, science des mouvements des points et des forces qui les provoquent, a été le premier chapitre de la physique qui a paru définitivement constitué. Depuis Galilée et Newton aucune modification n’a été faite dans ses principes, et on a pu espérer longtemps, malgré de nombreuses difficultés, que tous les autres chapitres de la physique parviendraient à cet état de perfection qu’avait atteint la mécanique.
Bien que plusieurs de ces chapitres, tels que l’électromagnétisme et l’étude du rayonnement, paraissaient rebelles, il y avait des choses qui paraissaient intangibles en physique : la géométrie, c’est-à-dire la science de la mesure des longueurs, la cinématique et la mécanique, sciences de la mesure du temps et du mouvement des corps.
La relativité
Les premiers coups portés à cette conception ont concerné la notion de temps. En 1905, Einstein proposa la théorie dite de la relativité restreinte. Cette théorie, basée sur une expérience faite par Michelson en 1880, modifiait simplement la manière dont deux observateurs mesuraient l’espace et le temps et liaient entre eux leurs mesures. Deux événements se produisant en des points différents de l’espace pouvaient être simultanés pour un observateur et non pour l’autre. L’énergie ne pouvait se déplacer avec une vitesse supérieure à celle de la lumière. Cette théorie était dite théorie de la relativité parce qu’elle affirmait en outre l’impossibilité de définir, par une convention quelconque,. un système de référence et de mettre en évidence le mouvement d’un observateur par rapport à ce système par des moyens expérimentaux, si ce mouvement se réduisait à une translation rectiligne uniforme. C’est ainsi par exemple, que le mouvement de translation du système solaire ne peut être défini d’une manière absolue. On peut constater que le soleil se déplace dans une certaine direction et avec une certaine vitesse par rapport à certaines étoiles, mais cela n’a aucun sens absolu, car on peut tout aussi bien dire que ce sont les étoiles qui se déplacent par rapport au soleil avec la vitesse opposée. On peut dire en un mot, que la théorie de la relativité restreinte proposée par Einstein en 1905 revenait à nier l’existence, c’est-à-dire la possibilité de constatation expérimentale d’un milieu nommé éther qui aurait pu servir de système de référence pour repérer les mouvements de tous les corps.
Si la relativité restreinte introduisait dans les notions d’espace et de temps des modifications si profondes, elle ne modifiait nullement la géométrie. Pour un observateur quelconque l’espace restait euclidien et infini.
II importe de dire que la relativité restreinte a été vérifiée par de nombreuses expériences et qu’elle représente de nombreux phénomènes avec plus d’exactitude que le faisaient les notions d’ espace et de temps absolus.
Les géométrie non euclidiennes
Nous avons fait tout à l’heure une distinction entre la géométrie et l’édifice logique ; nous avons parlé d’édifice euclidien et dit que l’espace physique paraissait euclidien. Montrons maintenant d’une part que l’on peut imaginer des édifices logiques non euclidiens, et d’autre part qu’il n’est pas absurde
a priori
de penser que l’espace dans lequel nous vivons pourrait ne pas être euclidien.
Dans ce domaine, les théoriciens ont devancé les expérimentateurs : Lobatchevski, mathématicien russe, Bolyai, mathématicien hongrois, puis Riemann, célèbre mathématicien allemand, créèrent au début du XIXe siècle des édifiées géométriques non euclidiens.
Un édifice logique non euclidien est une suite de propositions partant d’axiomes différents de ceux de la géométrie euclidienne et s’enchaînant logiquement. La plupart des postulats et des résultats de ces géomètres étaient différents de ceux de la géométrie euclidienne. Dans la géométrie de Lobatchevski, par un point extérieur à une droite on peut mener une infinité de parallèles à cette droite et dans celle de Riemann on n’en peut mener aucune, alors que dans la géométrie euclidienne on pouvait en mener une et une seule (postulatum d’Euclide).
Signalons également que dans la géométrie de Lobatchevski et de Bolyai la somme des angles d’un triangle est inférieure à deux angles droits alors que dans celle de Riemann elle lui est supérieure.
On peut étahlir un résultat qui restreint le nombre des géométries. Si l’on impose à une géométrie d’admettre tous les déplacements possibles, en langage physique si l’ on admet la possibilité d’existence de corps solides possédant tous les degrés de liberté possibles, on a à choisir entre 3 géométries : la géométrie euclidienne, la géométrie de Lobatchevski et Bolyai et la géométrie de Riemann.
Quelque étrange que cela paraisse, il est facile de concevoir ces géométries non euclidiennes, tout au moins celle de Riemann, et il importe pour la compréhension de ce qui va suivre de dire quelques mots de cette dernière.
Nous allons montrer simultanément la possibilité de construction d’une géométrie Riemanienne et la possibilité pour l’univers physique d’être régi par cette géométrie.
Géométrie Riemannienne. Espace sphérique.

Il nous sera nécessaire, pour des raisons de commodité, de réduire à 2 le nombre des dimensions de l’espace sur lequel nous raisonnons, Comme nous établissons simultanément l’existence théorique et la possibilité physique de tels espaces, nous sommes obligés d’admettre, pour un instant et pour la commodité du langage, que les êtres humains sont des êtres à deux dimensions c’est-à-dire des êtres infiniment plats ; vivant sur une surface dont ils ne peuvent sortir. Malgré cette simplification, tout ce que nous dirons pourrait être étendu à un espace à trois dimensions et à un univers réel sans autres difficultés que celles provenant de longueurs de langage.
Puisque nous imaginons que les êtres humains et l’espace n’ont p1us que deux dimensions, la notion classique d’univers euclidien se confond avec celle de plan euclidien. D’après la théorie classique nous nous représentons donc les hommes comme étant des êtres plats se déplaçant sur un plan infini dans toutes les directions.
Imaginons maintenant que ces êtres plats au lieu de vivre sur un plan comme le suppose la théorie classique soient placés sur une sphère et que l’univers se réduise pour eux à la surface de cette sphère ; nous considérons naturellement qu’ils ne peuvent observer que des longueurs sur la sphère, des angles entre des lignes tracées sur la sphère, et qu’ils ne peuvent recevoir d’impression lumineuse, par exemple, que de rayons lumineux se déplaçant sur la sphère. Ces êtres que nous imaginons connaîtront des corps solides plats à deux dimensions ; avec ces corps, ils mesureront des longueurs et des angles. Ils observeront des rayons lumineux sur leur sphère et construiront une géométrie, le mot étant toujours pris dans le même sens de science expérimentale. Cherchons ce que sera cette géométrie.

Remarquons d’abord que la géométrie que ces êtres construiront obéit à la condition d’admettre des déplacements ; car, comme un plan, la sphère peut se superposer à elle-même par une infinité triple de déplacements. Il existe toujours un déplacement d’une sphère sur elle même ne changeant pas les longueurs et amenant un point donné de la sphère sur un autre point quelconque de celle-ci et une direction issue du premier point en coïncidence avec une direction quelconque issue du deuxième. Pour nous, observateurs de l’espace à 3 dimensions qui voyons ces êtres se déplacer sur leur sphère, ces déplacements se réduisent à des rotations autour du centre de la sphère.
Nos êtres appelleront « ligne droite » le plus court chemin d’un point à un autre ou, si l’on préfère, en termes techniques, les lignes géodésiques de leur univers : on sait que sur une sphère ces lignes sont des grands cercles c’est-à-dire des sections de la sphère par des plans passant par le centre ; Ils appelleront « distance entre deux points » la longueur de l’arc de grand cercle qui joint ces deux points. On sait que cette longueur est égale au produit du rayon de la sphère par l’angle sous lequel, du centre de celle-ci, on voit l’intervalle des deux points. S’ils adoptent comme définition de deux droites parallèles la définition classique, c’est-à-dire deux droites qui ne se rencontrent pas, il est facile de voir que par un point extérieur à une droite on ne pourra mener aucune parallèle à cette droite, car deux grands cercles d’une même sphère se rencontrent toujours en deux points diamétralement opposés (fig. 2). La géométrie que construiront nos êtres imaginaires sera la géométrie de Riemann, et l’on voit en même temps que l’édifice de la géométrie riemanienne n’est autre, si on le limite à deux dimensions, que la géométrie sphérique. Il est bien connu par exemple que la somme des angles d’un triangle sphérique est supérieure à deux droits, l’excès de cette somme sur deux droits étant égal à la surface du triangle (fig. 3).
Cette géométrie riemanienne paraîtra aux êtres qui vivent sur une sphère comme la plus naturelle, car elle sera conforme à leur expérience courante et toutes les observations précises qu’ils pourront faire ne feront que confirmer cette constatation.
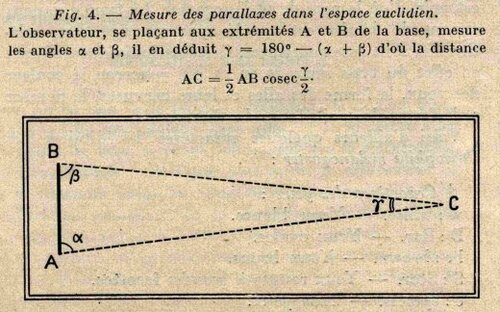
Signalons une particularité curieuse : on sait que pour évaluer la distance d’un point C que l’on ne peut pas atteindre, on mesure sa parallaxe : on prend une base AB perpendiculaire à la direction du point C (fig. 4). En A et B on mesure les angles α et β que font avec la base les droites AB et AC et l’on appelle parallaxe l’angle γ égal à $$$ 180^{o} - \alpha - \beta$$$. La connaissance de la longueur AB et de l’angle γ permet de calculer la distance du point C si on le suppose placé dans un espace euclidien.
Si les êtres que nous imaginons répétaient cette opération, ils trouveraient que la parallaxe du point C est positive tant que sa distance est inférieure à , qu’elle devient négative si la distance du point C à AB est supérieure à (fig. 5). Cet exemple nous montre clairement comment des observations faites sans quitter la sphère permettent de reconnaître que cette surface n’est pas plane et que la géométrie sur cette surface n’est pas la géométrie euclidienne, mais bien la géométrie riemanienne.
Signalons enfin la particularité qui peut nous paraître peut-être la plus curieuse et qui concerne l’infini physique pour des êtres vivant sur une sphère. Les êtres que nous avons imaginés traceront des lignes droites qui, nous l’avons dit, sont des grands cercles de la sphère et ils reconnaîtront que s’ils se déplacent sur ces lignes droites en marchant droit devant eux ils finiront par revenir à leur point de départ après avoir fait le tour de la sphère et avoir parcouru une longueur égale à $$$ 2 \pi R$$$ : longueur d’un grand cercle. Par exemple un être infiniment plat qui vivrait à la surface de la terre, qui partirait de l’Afrique vers l’Atlantique en suivant l’équateur, traverserait l’Amérique, le Pacifique et reviendrait à son point de départ en Afrique par le côté opposé de celui où il est parti.
Il nous est donc facile de concevoir, en nous limitant à des êtres à deux dimensions un univers fini et qui n’admet pas de bords. Il est un peu plus difficile de concevoir un espace à trois dimensions possédant les mêmes propriétés, mais la géométrie analytique, d’une manière plus précise la théorie mathématique des espaces métriques, nous permet de construire la géométrie d’un espace sphérique à trois dimensions. Dans un tel espace, si on marchait indéfiniment dans la même direction, on reviendrait à son point de départ après en avoir fait le tour : un tel espace est dit sphérique.
Par analogie avec l’exemple à deux dimensions que nous avons donné, on propose souvent, comme image d’un tel espace sphérique une sphère à trois dirnensions plongée dans un espace euclidien à quatre dimensions. Il faut bien dire que cette image est assez peu commode pour nous, car, si l’espace euclidien nous est familier, il n’en n’est pas de même de l’espace à quatre dimensions.
De plus, cette représentation de l’espace sphérique par une sphère de l’espace à quatre dimensions présente un assez grave inconvénient. Elle pourrait nous laisser croire qu’un espace sphérique à trois dimensions est nécessairement plongé dans un espace euclidien à quatre. Or il n’en n’est nullement ainsi et physiquement on peut très bien concevoir l’espace sphérique à trois dimensions en lui même sans faire appel pour cela à une quatrième dimension.
Croire que l’espace sphérique à trois dimensions est plongé dans un espace euclidien à quatre est une affirmation arbitraire et dont l’origine anthropocentriste est évidente. Elle est une ultime conséquence de l’habitude que nous avons contractée de ne concevoir facilement que l’espace euclidien.
Nous avons montré au contraire que toutes les propriétés métriques d’un espace peuvent être étudiées et définies entièrement sans quitter cet espace. C’est ainsi que l’on peut définir le rayon d’un espace sphérique sans le supposer pour cela placé dans un espace euclidien à une dimension de plus : imaginons que l’on fasse le tour de l’espace sur une ligne droite et que l’on revienne à son point de départ, on appellera rayon de l’espace le quotient par $$$ 2 \pi$$$ de la longueur du trajet parcouru.
Ainsi il n’y aurait aucune impossibilité, ni logique ni physique à ce que notre espace fût sphérique et des expériences physiques peuvent nous montrer s’il en est bien ainsi.
Espaces plus généraux - Relativité généralisée
Revenons à nos êtres infiniment plats et plaçons-les cette fois sur une surface quelconque, ces êtres construiront une géométrie qui sera la géométrie métrique de la surface sur laquelle ils vivent. En général leur géométrie n’admettra pas de déplacements. Sans insister sur ce point, signalons qu’à la fin du XIXe siècle, les mathématiciens, particulièrement en France, Darboux puis Cartan, ont abondamment développé cette théorie métrique des surfaces, et montré comment l’expression qui donne le carré de la distance de deux points infiniment voisins de la surface, ce que l’on appelle le ds², permet d’établir toutes ses propriétés géométriques. Ces théories peuvent s’étendre aux espaces à un nombre quelconque de dimensions, en particulier aux espaces à trois et quatre dimensions. On sait faire la géométrie des espaces non euclidiens les plus généraux.
Ces considérations n’avaient eu qu’un intérêt purement mathématique jusqu’en 1916, lorsque Einstein proposa la théorie de la relativité généralisée. Dans cette théorie, l’univers est un continuum non euclidien à quatre dimensions : trois d’espace et une de temps. Les propriétés métriques de ce continuum, c’est-à-dire la définition des longueurs et des intervalles de temps dans l’univers se trouvent fixées par ce que l’on appelle le ds² de l’univers.
La théorie d’Einstein consiste à poser les relations qui existent entre ce ds², la densité matérielle et la densité de mouvement en chaque point de l’univers. Bien que ce fait n’ait pas été établi en toute rigueur, on pense que les équations d’Einstein permettent de calculer le ds² sans ambiguïté une fois que l’on a donné la distribution de la matière dans l’univers et son mouvement.
On peut donner de cette théorie une image assez grossière. Reprenons nos êtres à deux dimensions vivant sur une surface, supposons cette fois la surface élastique et plaçons-la dans le champ de la pesanteur. On peut se représenter la matière comme des poids répartis sur cette surface et l’on comprend que celle-ci soit déformée par les poids et que sa métrique, c’est-à-dire la mesure des longueurs des courbes tracées sur cette surface, puisse être calculée lorsqu’on connaît la répartition des poids ; par exemple, si la surface est libre de toute masse, elle prendra une forme plane, et des êtres vivants à sa surface se croiront dans un espace euclidien. Si l’on place une grosse masse en un point, la surface se creusera en ce point et dans son voisinage ; nos êtres imaginaires observeront que leur univers n’est plus euclidien, mais qu’il présente une courbure et ils se sentiront attirés vers la masse.
Un autre point important de la théorie d’Einstein est ce fait que la mécanique apparaît comme un chapitre de la géométrie, car le mouvement des points matériels se trouve défini lorsqu’on connaît le ds² de l’univers. On impose aux points matériels la condition de suivre les lignes de plus court chemin.
On sait que cette théorie d’Einstein a été l’objet de trois vérifications qui semblent assez bonnes.
Nous avons dit que le ds² de l’univers, ou si l’on préfère sa métrique, se trouve conditionné par la densité et le mouvement de la matière en chacun de ses points. Les équations d’Einstein qui établissent ces conditions contiennent deux constantes inconnues et un éminent géomètre français, M. E. Cartan a montré que les équations écrites par Einstein étaient les seules que l’on pouvait formuler, si l’on imposait à ces équations la condition de comporter comme conséquence les équations de la mécanique. On conçoit qu’il soit très important de connaître les valeurs de ces deux constantes arbitraires. L’une d’elles est connue avec grande exactitude, car elle n’est autre que le coefficient de l’attraction newtonienne.
Jusqu’à présent l’expérience ne nous a pas permis de déterminer la seconde.
Structure macroscopique de l’univers d’après la théorie d’Einstein
Nous entendons par structure macroscopique de l’univers la métrique de cet univers lorsqu’on se place à une très grande échelle, c’est-à-dire lorsqu’on néglige les petits accidents locaux qui peuvent intervenir. Nous allons préciser tout à l’heure à quelle échelle il faut se placer pour cela. Prenons un exemple : on sait qu’un gaz est composé de molécules, séparées par des vides d’autant plus grands que la densité est plus faible, douées d’une agitation désordonnée ; étudier un gaz en considérant isolément ses molécules, c’est faire son étude microscopique ; étudier un gaz en considérant l’action totale et les propriétés globales de milliards de molécules, c’est faire son étude macroscopique. Pour faire cette étude, on se placera à une échelle suffisamment grande. Par exemple, on considérera que le mm est une petite longueur. Supposons que l’on veuille évaluer la force qui s’exerce en chaque point du gaz, on étudiera pour cela le mouvement d’une masse et on cherchera son accélération et comme on se place au point de vue macroscopique, on adoptera pour valeur de l’accélération la moyenne de celle-ci sur un mm de la trajectoire et non pas sur 1/100 000 de mm. On conçoit en effet que sur un intervalle de 1/100 000 de mm, la force exercée sur le point puisse être troublée par des perturbations locales alors que sur un intervalle de 1 mm la moyenne de ces perturbations est toujours pratiquement la même.
On voit que pour considérer l’univers d’un point de vue macroscopique, il faut se placer à une échelle telle que la densité de la matière dans l’univers apparaisse comme constante ; nous verrons tout à l’heure qu’une telle échelle suppose que les plus petits déplacements que l’on effectue sont de plusieurs millions de fois les dimensions de la Voie lactée. A une telle échelle, l’univers physique apparaît comme rempli uniformément de matière, c’est à-dire celle-ci ayant une densité et une agitation identiques en tous ses points. On peut alors chercher quelle doit être, d’après la théorie d’Einstein, la structure géométrique d’un tel univers. Voici le résultat que l’on trouve.
L’espace doit être sphérique, son rayon dépend de la densité matérielle et de la constante cosmogonique, le temps a une signification absolue. Un tel univers est appelé : univers d’Einstein. Le fait que dans cet univers il existe un temps absolu m’a rien de contraire au principe de relativité. C’est la conséquence du fait qu’il existe un système de référence privilégié, celui qui est lié à la matière.
Une telle conséquence de la théorie d’Einstein n’a rien d’impossible, car il est certain que si notre espace est sphérique son rayon doit être très grand ; aussi avons-nous pu croire jusqu’à présent que l’espace était euclidien. Montrons-le en prenant l’analogie d’êtres infiniment plats à deux dimensions vivant sur une sphère.
Supposons que le rayon de cette sphère soit très grand par rapport à la région que nos êtres peuvent explorer. Cette région explorée sera très voisine d’un plan pour la même raison qui fait qu’en première approximation une petite région de la surface de la terre nous apparaît comme plane. Nos êtres imaginaires se croiront donc d’abord sur un plan et construiront d’abord une géométrie euclidienne ; mais ils pourront se rendre compte qu’ils vivent sur une sphère lorsque leurs observations deviendront plus précises ou lorsqu’elles s’étendront à une région suffisamment étendue.
Explorons donc l’espace et cherchons ce que l’astronomie peut nous dire à ce sujet.
L’univers astronomique
Dans cette revue rapide de l’univers qui nous entoure, nous nous attacherons particulièrement aux distances et nous chercherons à aller le plus loin possible. Partons de la terre qui est un globe de 6378 km de rayon, allons vers le soleil qui est à une distance de 23 400 fois le rayon de la terre, puis allons aux limites du système solaire, la distance de la planète la plus éloignée est une trentaine de fois la distance de la terre au soleil ; ce monde solaire qui a pourtant des dimensions très restreintes dans l’univers est déjà grand à notre échelle humaine, la lumière à la vitesse de 300 000 km/sec met une douzaine d’heures pour le traverser. Un homme marchant à une allure de 6 km à l’heure mettrait 200 000 ans pour effectuer le même trajet.
Pour évaluer les distances stellaires, on emploie une unité qui s’appelle le parsec. Le parsec est la distance à laquelle on voit le rayon de l’orbite terrestre supposé perpendiculaire au rayon visuel sous un angle d’une seconde. La lumière met un peu plus de trois ans à par courir un parsec. Les étoiles les plus proches de nous sont à quelques parsecs.
On sait que le soleil qui n’est qu’une étoile parmi des milliards d’autres est plongé dans un système stellaire appelé Voie Lactée ou Galaxie.
Le problème de la structure de la Voie Lactée est un de ceux qui préoccupe à juste titre les astronomes. Sans entrer dans les détails des recherches effectuées à ce sujet disons que la Galaxie est un amas stellaire de forme aplatie et sans doute spirale ou qu’il est peut-être formé d’une agglomération de quelques systèmes analogues.
Pour mesurer les distances des astres de la Voie Lactée on a d’abord employé la méthode des parallaxes dont nous avons dit un mot précédemment, mais bien vite on s’est aperçu que cette méthode était insuffisante, car elle ne permet d’évaluer que la distance des astres très proches. Pour sonder l’univers à des profondeurs suffisantes il fallut employer d’autres méthodes. Leur principe est photométrique ; on mesure l’éclat apparent d’un astre dont on connaît par ailleurs l’éclat absolu, c’est-à-dire l’éclat qu’il aurait s’il était placé à l’unité de distance .
La comparaison de ces deux éclats fournit la distance de l’astre étudié. On sait ainsi que la Voie Lactée dans sa plus grande dimension a 60000 parsecs de diamètre, la lumière met plus de 200000 ans à la parcourir de part en part. Le nombre des étoiles de la Voie Lactée est d’une trentaine de milliards, sa masse totale est de quelques dizaines de milliard de soleils.
Au delà de la Voie Lactée se trouvent d’autres astres appelés nébuleuses extragalactiques, ou plus souvent nébuleuses spirales. Ce sont des amas d’étoiles analogues à notre Galaxie, le plus proche est à 360000 parsecs et les plus petites nébuleuses spirales que l’on ait pu observer sont à environ 100 millions de parsecs. De telles distances sont très grandes par rapport à celles que nous considérons dans la vie courante : la distance des nébuleuses lointaines est de 3 millions de milliard de kilomètres, Le nombre des spirales connues est d’environ un million et il semble que dans les parties de l’univers que nous avons pu explorer jusqu’à présent les spirales soient réparties à peu près uniformément ; en tous cas il ne semble pas que leur nombre par unité de volume aille en diminuant quand on s’éloigne de la Voie Lactée.
Malgré l’étendue du monde exploré il n’a pas été possible jusqu’à présent, par des mesures de longueur ou d’angle, de vérifier si notre univers est euclidien ou non. En particulier il n’est pas possible de mettre en évidence des parallaxes négatives, car ces dernières seraient beaucoup trop petites et bien hors de portée de nos possibilités de mesure. Par contre un résultat nouveau et tout à fait inattendu concernant les mouvements des plus lointains de ces astres a été récemment observé et a jeté une lumière nouvelle sur la structure de notre univers et sur son évolution.
Les vitesses radiales
On sait mesurer par un procédé spectroscopique la vitesse radiale des astres, c’est-à-dire leur vitesse d’approche ou d’éloignement suivant la droite qui joint l’observateur à l’astre étudié et qui est appelée le rayon vecteur. Lorsqu’une source lumineuse s’éloigne d’un observateur, la longueur d’onde des rayons lumineux qui parviennent à celui-ci se trouve augmentée par rapport à la longueur d’onde émise par la source et l’augmentation est proportionnelle, en première approximation, à la vitesse de la source. Si au contraire la source s’approche avec la même vitesse, la longueur d’onde se trouve diminuée de la même quantité,c’est le phénomène connu sous le nom d’effet Doppler Fizeau.
Effectivement on a observé cet effet dans le spectre des étoiles et on a pu mettre en évidence ainsi les vitesses radiales des étoiles. La mesure du déplacement des raies dans les spectres stellaires par rapport aux mêmes raies du spectre d’une source terrestre donne directe ment la vitesse radiale des étoiles en km/sec.
Il y a une dizaine d’années on a tenté de mesurer les vitesses radiales des nébuleuses spirales et dès le début on a remarqué que ces dernières avaient tendance en général à s’éloigner de la voie lactée comme si celle-ci exerçait une répulsion sur elles. Devant ce curieux résultat, les astronomes américains Hubble et Humason tentèrent au Mont Wilson de déterminer les vitesses radiales de spirales aussi faibles que possible. C’était là un problème rendu difficile par la faiblesse de la lumière que nous envoient ces astres et il fallut pour y arriver construire des spectrographes spéciaux. L’instrument utilisé était le télescope de 2,50 m du Mont Wilson, la chambre photographique du spectographe était ouverte à F/0,6 et la dispersion n’était que 875 Å au mm à 4500 Å. Avec cet instrument Hubble obtint les spectres de nébuleuses spirales de 19e grandeur, c’est-à-dire les nébuleuses les plus faibles que l’on puisse photographier. Les poses duraient jusqu’à 30 heures et se faisaient naturellement en plusieurs nuits. Bien que les nébuleuses spirales soient composées d’un très grand nombre d’étoiles de natures différentes, leur spectre global présente un caractère stellaire ; on y voit en particulier les deux raies H et K du calcium ionisé qui sont très intenses dans le soleil, et on peut, grâce à cette circonstance, mesurer leur vitesse radiale avec une erreur qui, dans le cas des observations de Hubble, allait de 25 à 300 km par seconde.
Le résultat obtenu par Hubble est le suivant :
Les nébuleuses spirales s’éloignent de nous avec une vitesse proportionnelle à leur distance comme le montre le tableau ci-dessous :
| Nébuleuses | Nombre | Distance en millions de parsecs | Vitesse radiale en km/sec |
| isolées | 21 | 1,2 | 630 |
| Amas de la Vierge | 7 | 1,8 | 890 |
| isolées | 16 | 3,3 | 2 350 |
| Pisces | 4 | 6,9 | 4 630 |
| Pegasus | 5 | 7,2 | 3 810 |
| Cancer | 2 | 9,1 | 4 820 |
| Perseus | 4 | 10,9 | 5 230 |
| Coma | 3 | 14,4 | 7 500 |
| Ursa major | 1 | 22,9 | 11 800 |
| Leo | 1 | 36,3 | 19 600 |
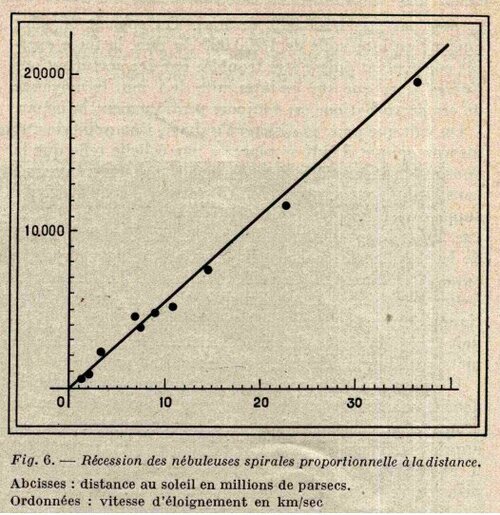
La figure 6 montre nettement cette proportion. La distance des nébuleuses spirales a été évaluée en mesurant leur éclat apparent. On voit que la nébuleuse la plus lointaine dont on ait pu mesurer la vitesse radiale, une petite nébuleuse de la constellation du Lion, s’éloigne de nous à la vitesse de 20000 km/sec, le 1/15 de la vitesse de la lumière. La réalité de ce phénomène ne fait aucun doute.
Quelle peut être l’origine de ce déplacement ? Nous allons voir que la théorie d’Einstein l’explique.
Univers en expansion
Pour expliquer ces phénomènes, de Sitter avait déjà proposé en 1917 une solution des équations d’Einstein qui supposait l’univers sphérique dans l’espace et dans le temps. L’univers de de Sitter, sur lequel nous n’insisterons pas, car l’exposé de ses propriétés est véritablement trop difficile sans symbole mathématique, expliquait la récession des spirales que l’on commençait à constater à cette époque, il présentait le défaut de supposer l’univers vide de matière. La solution du problème a été donnée par Friedman en 1922, puis reprise par Lemaitre en 1927 ; elle est basée sur cette remarque que l’univers d’Einstein, c’est-à-dire un espace sphérique rempli de matière ayant une densité uniforme vérifiant les équations d’Einstein, peut exister en effet mais est instable.
Rappelons par un exemple ce que l’on entend par instabilité d’une position d’équilibre : considérons une surface convexe tournant sa convexité vers le haut et plaçons une petite bille sur cette surface. Le point le plus élevé de la surface sera manifestement une position d’équilibre pour la bille, puisque si on place la bille en cet endroit sans lui donner de mouvement, elle y restera indéfiniment, mais on conçoit aussi que cette position soit instable, la moindre perturbation déplacera la bille et dès que celle-ci aura quitté sa position d’équilibre, elle s’en éloignera de plus en plus vite.
Si l’on reprend les équations d’Einstein en supposant cette fois que l’espace est sphérique, mais que son rayon est variable avec le temps, on s’aperçoit que ces équations sont vérifiées si les variations du rayon en fonction du temps suivent une certaine loi. Il n’est pas possible actuellement de préciser
a priori
la forme de cette loi, car elle dépend de la masse totale de l’univers et de la constante cosmogonique. On sait seulement quelles formes cette loi peut prendre.
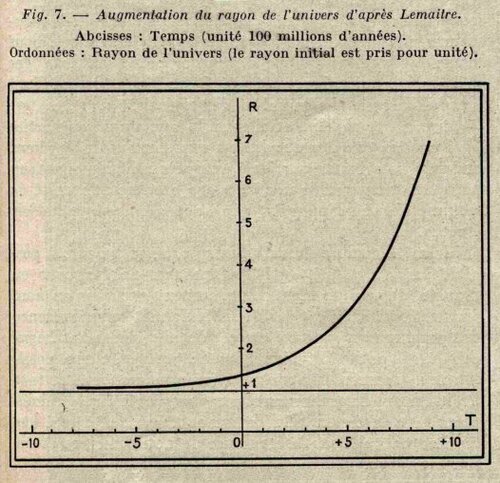
L’une de ces formes, qui est représentée sur la figure 7 et à laquelle Lemaître s’est attaché particulièrement, consiste en ceci : le rayon de l’univers part d’une valeur initiale au temps $$$ - \infty$$$ , valeur qui correspond à un espace d’Einstein en équilibre instable et à mesure que le temps augmente, le rayon de l’univers augmente indéfiniment.
Il existe d’autres formes de solution : l’une d’elles consiste en ce que le rayon de l’univers oscille périodiquement entre une certaine valeur et zéro. Il est évidemment impossible d’admettre que le rayon de l’univers puisse devenir nul ; d’ailleurs s’il devenait suffisamment petit, l’univers ne pourrait plus être considéré d’un point de vue macroscopique, et l’étude simplifiée que nous en avons faite cesserait d’être valable ; on admet donc que dans cette deuxième forme de variation du rayon, ce dernier oscille entre deux valeurs dont l’une est très petite.
Enfin dans une troisième forme de variation le rayon de l’univers serait primitivement infini, décroîtrait jusqu’à une valeur très petite, puis augmenterait indéfiniment.
Les phénomènes constatés par Hubble se trouvent expliqués par la théorie d’Einstein.
On peut montrer en effet que si l’univers était sphérique et si son rayon allait en augmentant avec le temps, un observateur quelconque verrait les astres qui l’entourent s’éloigner de lui avec des vitesses proportionnelles à leurs distances. Si l’on veut reprendre l’analogie du début, nous devons comparer les hommes à des êtres infiniment plats qui vivraient sur une sphère élastique, le rayon de la sphère variant suivant une certaine loi ; actuellement le rayon augmenterait. Il est manifeste que dans ces conditions les divers points de la sphère paraîtraient s’éloigner les uns des autres, les observateurs assisteraient à une dilatation d’ensemble de leur univers.
Données numériques
Comme nous l’avons dit, il est difficile de préciser numériquement les circonstances dans lesquelles se trouve notre univers, car nous sommes dans l’ignorance de la constante cosmogonique. On peut cependant donner quelques ordres de grandeurs : si notre univers était un univers d’Einstein en équilibre, son rayon ne dépendrait que de la densité moyenne de la matière. En adoptant pour celle-ci un chiffre moyen, on trouve un rayon de 718 millions de parsecs. Le domaine de l’univers que nous avons pu explorer est donc une faible partie de celui-ci.
Dans une autre solution adoptée par Lemaitre, le rayon initial de l’univers aurait été de 364 millions de parsecs. Il serait actuellement d’environ 1500 millions de parsecs, actuellement il doublerait en 1500 millions d’années.
Signalons enfin que, dans un fort curieux travail, l’éminent astronome anglais sir Arthur Eddington a donné une évaluation de la constante cosmogonique basée sur l’analogie qui existe entre deux termes de l’équation de Dirac de la mécanique ondulatoire. Ce travail est trop récent et n’a pas encore reçu de vérification ni d’application, aussi le laisserons-nous provisoirement de côté.
Univers infini en expansion
Récemment, Einstein a montré que l’univers pouvait avoir une structure toute différente de celle que proposait Lemaitre : les équations d’Einstein se trouvent vérifiées par un espace euclidien, infini dans toutes les directions, mais dans lequel les distances entre les corps se dilatent suivant une certaine loi. La théorie nous conduit donc à admettre aussi bien que l’univers est fini ou qu’il est infini, mais l’expérience nous oblige à admettre qu’il se dilate.
Les événements inconnaissables
Pour terminer, signalons une curieuse propriété de l’univers en expansion. Dans un tel univers, tout observateur a le droit, au point de vue mécanique, de se supposer fixe, les autres corps s’éloignant de lui avec une vitesse proportionnelle à la distance. Pour une augmentation de la distance de 1 million de parsecs, l’augmentation de la vitesse d’éloignement est de 558 km/sec. C’est ainsi que les astres situés à 1 million de parsecs s’éloignent avec une vitesse de 558 km/sec, que les astres situés à 100 millions de parsecs s’éloignent avec une vitesse de 55 800 km/sec, et que les astres situés à une distance de 538 millions de parsecs s’éloignent de nous avec une vitesse de 300000 km/sec, c’est-à-dire avec la vitesse de la lumière. Quant aux astres situés plus loin, leur vitesse d’éloignement est supérieure à celle de la lumière.
Il ne faut pas voir là une contradiction avec le principe de relativité restreinte, car ce principe affirme simplement que deux corps voisins dans l’espace et dans le temps ne peuvent se déplacer l’un par rapport à l’autre avec une vitesse supérieure à celle de la lumière. Dans le cas que nous considérons actuellement il s’agit d’un phénomène différent : la longueur d’espace qui sépare notre système solaire d’une nébuleuse extrêmement lointaine augmente avec une vitesse supérieure à celle de la lumière ; cette vérité n’a qu’un sens d’interprétation mais ne correspond pas à la possibilité pour nous d’effectuer des échanges d’énergie avec les corps qui se déplacent avec une vitesse supérieure à celle de la lumière.
La particularité que nous voulons signaler est la suivante.
Les événements qui se produisent sur les astres situés actuellement à plus de 538 millions de parsecs sont inconnaissables pour nous, car il n’existe pas de possibilité de communication entre ces événements et nous. Le principe de relativité restreinte nous apprend qu’en effet aucun signal ne peut se déplacer avec une vitesse supérieure à celle de la lumière ; par conséquent, tout signal qui nous serait envoyé en ce moment de l’un de ces astres ne pourrait nous parvenir puisqu’il se déplacerait moins vite que n’augmenterait la distance entre lui et nous .
Telles sont les conclusions auxquelles nous conduit provisoirement la science moderne. L’univers que nous croyions euclidien autrefois ne l’est sans doute pas, et l’expérience nous montre qu’il se dilate homotétiquement. L’avenir nous dira sans doute très prochainement quelle est exactement la forme de l’univers et quels sont son passé et son avenir. On ne peut s’empêcher d’admirer, malgré bien des tâtonnements et des erreurs, la puissance prodigieuse de l’esprit humain ; limités comme nous le sommes à des déplacements à la surface de notre petit globe ; nous parvenons à concevoir la structure du monde immense qui nous entoure et avec lequel nous n’avons que de fugitives communications par la pâle lueur qui nous vient des étoiles. Cette constatation nous donne confiance dans l’avenir.
Henri Mineur, Astronome à l’Observatoire de Paris.
Pour en savoir plus
- Albert Einstein : La relativité - petite bibliothèque payot
- O. Costa de Beauregard : La théorie de la relativité restreinte - Masson -1949
- André Troller : Einstein et les théories de la relativité ,La Nature N°2492 - 7 janvier 1922
- Ch. de La Vallée Poussin : La relativité restreinte (suite des articles « La notion de temps et la physique ») La Nature N°2642 - 22 Novembre 1924
- Les théories de la relativité : Les expériences de Miller - Les observations du Dr Adams - La Nature n°2684 - 12 septembre 1925
- Louis Warnant : État expérimental actuel des bases de la théorie de la relativité restreinte - La Nature n°2684 - 12 septembre 1925
- J.M. Chevallier : Le cinquantenaire de la relativité : La leçon d’EINSTEIN, Atomes N°109 - Avril 1955
- Jean-Marc Lévy-Leblond : Le radar doit permettre une nouvelle vérification de la relativité générale, La Nature N° 3359 - Mars 1965
- Albert Ducrocq : L’aberrascope : prochaines expériences sur la relativité - Atomes N°225, Octobre 1965
- André Regnier : La relativité et la philosophie - Atomes N°233, Juin 1966
- France Noël : Relativité et mouvement des planètes, Atomes N°244 - Juin 1967
- Armand-Jocellyn Vébel : La relativité générale : science (enfin) expérimentale, La Recherche N°9 - Février 1971
- James Lequeux : La relativité générale vérifiée, La Recherche N°34 - Mai 1973
- Sylvain Clément : Le second postulat de la relativité : un test décisif, La Recherche N°94 - Novembre 1978
- Jean-Marc Lévy-Leblond : La relativité aujourd’hui, La Recherche N°96 - Janvier 1979
- Jean-Paul Desclaux, Pekka Pyykkö : Quand la chimie rejoint la relativité, La Recherche N°111 - Mai 1980
- Thibault Damour : Le renouveau de la relativité générale, La Recherche N°189 - Juin 1987
- Gérard Petit, Peter Wolf : Tester la relativité sans quitter son fauteuil, La Recherche N°297 - Avril 1997
- Peter Galison : Le train fantôme de la relativité restreinte - Le Temps, Dossier N°5 de La Recherche - Avril 2001
- Elisa Brune, Philippe Mergny : La relativité restreinte , La Recherche N°353 - Mai 2002
- Relativité générale : pourquoi deux preuves n’ont pas suffi (entretien avec Jean Eisenstaedt) , Stéphanie RUPHY - La Preuve Scientifique, Dossier N°8 de La Recherche - Juillet 2002
- L’héritage Einstein :1905-2005 Un siècle de physique, Dossier N°18 de La Recherche - Février-Avril 2005
- Peter Galison : Einstein-Poincaré : Deux savants pour la relativité, La Recherche N°383 - Février 2005

