La voiture électrique est devenue en France, à l’heure actuelle, une nécessité, au moins provisoire. Alors que des essais se poursuivent de tous côtés, il n’est peut-être pas inutile de faire connaître quels résultats on peut raisonnablement en attendre. Nous verrons, d’ailleurs qu’une telle étude ne dispense en aucune manière de faire des essais pratiques, car les caractéristiques à donner au moteur et à l’installation d’une voiture dépendent de compromis entre diverses qualités dont les unes peuvent se chiffrer et les autres simplement s’apprécier.
La première chose à l’aire est de rassembler les données nécessaires pour évaluer la puissance demandée par le roulement.
Puissance nécessaire au roulement.
D’abord les chiffres pratiques : les anciens essais faits en diverses occasions, d’abord vers 1900, puis vers 1922-23, ont montré que les voitures électriques roulant dans Paris ont consommé en moyenne d’abord 80 Wh par tonne-kilomètre, chiffre qui a été abaissé à 65 Wh en 1923 pour de petits véhicules pesant environ 2 tonnes en ordre de marche, et même à 55 Wh pour des camions de charge utile dépassant 2 tonnes. Ces chiffres tiennent compte des diverses circonstances que l’on rencontre dans la marche dans Paris : arrêts forcé aux carrefours, embouteillages, côtes réparties sur les trajet, etc., et ils ont trait à des véhicules donnant sur un parcours prolongé une vitesse moyenne de 20 km/h environ. Il s’agit des Wh pris aux accumulateurs, et non des Wh débités par le poste de recharge, qui introduit encore un rendement important. Si l’on veut intégrer le chiffre de 65 Wh par tonne.km, on trouve, par un calcul simple, qu’il représente l’énergie à dépenser pour monter, avec un rendement unité, une côte permanente de 2,4 %, Si l’on compte avec un rendement ρ à partir des accumulateurs (ρ=rendement du moteur x rendement de la transmission) on trouve naturellement l’équivalent d’une côte de pente 2,4 ρ %. Si, par exemple, on admet ρ=0,7, on a comme pente équivalente, 1,7 % ; ce qui est vraiment faible.
Prenons maintenant les données connues sur les coefficients de traction : les meilleurs coefficients sont obtenus sur l’asphalte, et ils correspondent à un frottement de 1 à 1,5 %. Le pavé, le macadam donnent déjà 2 %, Sur les mauvaises routes, on peut monter à 8 et même 16 %, Ces chiffre correspondent à un roulement exécuté dans de bonnes conditions, par exemple avec des bandages pleins. S’il agit de pneumatiques, il est nécessaire que ceux-ci soient très gonflés pour atteindre sur l’asphalte des coefficients aussi bas que ceux que nous avons cités.
Dès que la vitesse s’accroît un peu, il faut en outre tenir compte de la résistance de l’air. On peut admettre en moyenne que l’équilibre de la puissance dépensée pour vaincre la résistance de roulement s’obtient vers 60 km/h. Comme la résistance due à l’air croit comme le carré de la vitesse, on est conduit à admettre connue expression générale du coefficient de frottement s’opposant à la marche :
$$$ f= \frac{1,5}{100} [1 + ( \frac{v}{60})^2]$$$
v étant la vitesse en km/h
Il est alors commode de calculer les chiffres du tableau suivant :
Ceci permet d’obtenir les puissances nécessaires pour rouler en terrain plat ou en côte, à une vitesse de v km/h et avec un certain rendement de transmission : nous admettrons un rendement de transmission de 0,85, et nous obtiendrons, suivant les conditions de roulement (vitesse et côte), les puissances mécaniques en chevaux par tonne qu’il est nécessaire que le moteur délivre :
| Plat | 3% | 6% | 9% | 12% | |
| 5 km/h | 0,33 | 0,98 | 1,63 | 2,27 | 2,92 |
| 10 - | 0,66 | 1,96 | 3,27 | 4,6 | 5,9 |
| 15 - | 1 | 2,96 | 4,94 | 6,87 | |
| 20 - | 1,34 | 3,95 | 6,56 | ||
| 25 - | 1,92 | 5,18 | |||
| 30 - | 2,45 | 6,37 | |||
| 35 - | 3,05 | ||||
| 40 - | 3,76 |
On peut représenter ces résultats en traçant de courbes à puissance constante sur un diagramme — pente de la route, vitesse — et l’on obtient les courbes figurées ci-dessous, qui permettent de déterminer la vitesse qu’il est possible d’obtenir sur une côte donnée en appliquant une puissance donnée.
Il reste à savoir maintenant dans quelle mesure ces chiffres s’appliquent à la réalité. Il est hors de doute qu’ils s’appliquent bien, mais à de très bonnes voitures roulant dans de très bonnes conditions. Si, en effet, nous prenons une voiture roulant à 20 km/h nous trouvons sur le tableau précédent qu’elle roule avec un frottement équivalent à 1,66 %, alors que la pratique nous a appris qu’elle dépensait 65 Wh par tonne.km, ce qui, avec un rendement total de 0,7, correspondrait bien à une côte de 1,7 à gravir.
Dans la pratique il faut prendre de forts coefficients majorant les puissances ainsi trouvées :
- du fait de parcours moins favorables pouvant donner lieu à une plus grande proportion de côtes à monter ;
- du fait d’un vent debout, toujours possible, qui pourrait augmenter notablement la résistance à vaincre ;
- enfin, du fait que la voiture n’est que rarement en régime permanent et qu’elle a souvent à accélérer.
De plus, quand il s’agit de voitures électriques transformées de voitures à essence, on a en général des quantités de pertes au roulement tenant à des procédés ou à des réglages plus ou moins barbares dans la transmission, qu’il aurait été facile d’éviter, qui en fait étaient négligeables vu le grand excès de puissance des moteurs à explosion, mais qui deviennent singulièrement grandes dans le cas de la traction électrique où la puissance est sérieusement mesurée.
L’accélération
La question de l’accélération, du degré de nervosité à demander aux démarrages d’une voiture, demande à être examinée.
Supposons une voiture qui roule à 35 km/h en palier dans les conditions du tableau précédent, c’est-à-dire surmontant un frottement de 2 %. Donnons subitement au moteur un couple double : ce couple sera employé pour moitié à vaincre le dit frottement, pour moitié à accélérer la voiture. L’accélération prise va être γ telle que mγ = 2/100 mg
m étant la masse de la voiture et g l’accélération de la pesanteur. D’où γ = 2/100 g ≈ 20 cm/s² puisque g vaut sensiblement 10 m/s².
Donc, la vitesse de la voiture, qui était déjà de 36 km/h, soit 10 m/s, va augmenter à raison de 20 cm/s toutes les secondes : c’est dérisoire et, pour obtenir ce piteux résultat, il a cependant fallu doubler la puissance.
Telle est la raison pour laquelle on met sur les voitures des moteurs à essence huit ou dix fois plus puissants que ce qui suffirait à leur donner leur vitesse de régime en ville.
Pour les voitures électriques, la question se présente très différemment : en principe, le moteur électrique tolère de grandes surcharges pendant des temps pas trop longs, mais il faut l’examiner du point de vue de sa capacité à fournir de forts couples.
Les possibilités des accumulateurs
Nous ne parlerons ici que des accumulateurs au plomb, car les accumulateurs cadmium-nickel sont pratiquement inaccessibles à l’heure actuelle.
La batterie normale de démarrage des voitures à essence est dite de 6 volts 90 Ampères-heure (Ah), elle pèse sensiblement 23 kg. On pourrait donc croire qu’elle contient 6x90=540 Wh, et qu’il faut par conséquent admettre qu’on peut obtenir 540/23 ≈ 23 Wh/kg d’accumulateur.
Mais en réalité les 90Ah s’entendent pour une décharge en 10 heures. Si la batterie se décharge plus vite, la capacité baisse, et ceci dans un rapport Indiqué par le tableau ci-dessous :
| Durée de décharge | 10h | 5 h | 4 h | 3 h | 2 h | 20 min |
| Capacité relative | 1 | 0,85 | 0,82 | 0,75 | 0,65 | 0,33 |
Pour une voiture électrique capable de marcher environ 2 heures sans recharge, nous aboutissons donc à la conclusion que la capacité n’est plus que de 23 x 0,65 = 15 Wh/kg.
En réalité, la situation n’est pas tout à fait aussi noire, car si on arrête la décharge de temps en temps, l’acide reconstitue par diffusion la capacité et, au cours d’une série de décharges partielles rapides mais espacées pour durer en tout 10 h, une batterie retrouve une capacité voisine de sa capacité théorique de décharge lente en 10h.
Par conséquent, une voiture électrique est avantagée par un service comportant des arrêts fréquents.
Mais les batteries de démarrage ne sont pas de bons exemples d’accumulateurs à employer pour la traction. Elles ont été réalisées, en effet, pour répondre à des desiderata particuliers aux constructeurs d’automobiles, et leur faible encombrement ainsi que leur légèreté relative est obtenue en diminuant l’épaisseur de leurs plaques positives d’une manière telle que leur vie est limitée à environ 150 cycles complets de charge et de décharge.
Il existe des batteries plus légères encore : ce sont les batteries d’avion : là, la légèreté est obtenue en diminuant la quantité d’électrolyte en jeu. Les véritables batteries de traction sont plus lourdes, mais en contrepartie elles sont garanties pour un plus grand nombre de cycles de décharges : de 600 à 800 environ.
A l’heure actuelle, les constructeurs s’efforcent de mettre à la disposition des usagers de la voiture électrique des batteries de traction dites légères ou de semi-traction, qui auraient une vie garantie pour 350 cycles de décharge environ. Il semble qu’avec ces batteries on puisse compter sur 23 Wh/kg pour une décharge en 2 heures dans les meilleures conditions, soit 26,5 Wh pour une décharge en 3h, On ne sait pas bien encore quelles seront les performances pratiques de ces batteries. Il est à supposer que leur légèreté a été obtenue au détriment de la quantité d’électrolyte, et que le niveau d’eau, dans leurs compartiments, aura besoin d’être soigneusement surveillé.
Le bilan des poids pour une voiture de performances données
Puisque nous connaissons, par des chiffres pratiques, les Wh nécessaires pour accomplir un trajet donné avec un véhicule de poids donné, ainsi que le poids des accumulateurs rapportés aux Wh qu’ils contiennent, nous pouvons immédiatement prévoir le rayon d’action.
Soit une voiture pour laquelle le rapport du poids des accumulateurs au poids de la voiture est λ. Nous nous baserons sur de bonnes batteries donnant par kg d’accumulateur :
| 15 Wh pur une décharge en 1h |
| 20 Wh pour une décharge en 2 h |
| 22,5 Wh pour une décharge en 3 h |
| 15 Wh pour une décharge en 4 h |
Nous admettrons le chiffre moyen (favorable) de 65 Wh par tonne.km, et nous trouvons comme rayon d’action en kilomètres (chiffres optimistes) :
| Régime de | Rayon | λ=1/3 | λ=1/4 | λ=1/5 | λ=1/6 |
| 1h | 158λ km | 53 | 4O | 32 | 26 |
| 2h | 208λ km | 70 | 52 | 42 | 35 |
| 3h | 125λ km | 75 | 56 | 45 | 37,5 |
| 4h | 160λ km | 83 | 65 | 52 | 43 |
Pratiquement nous connaissons une voiture qui vient d’être transformée, pesant en ordre de marche, avec son conducteur, 650 kg, sensiblement, dont 160 kg. d’accumulateurs. Elle a un rayon d’action qui atteint ou dépasse 62 km quand eue est utilisée a faire des courses dans Paris. Ceci correspond à &lambda=13,6 et tombe en somme assez bien dans les chiffre du tableau précédent.
On voit donc qu’il faut compter avoir sur la voiture en ordre de marche sensiblement le quart ou le tiers du poids de la voiture en accumulateurs pour avoir des performances raisonnables avec une vitesse moyenne restant faible. Pour les voitures neuves, à construire, on peut concevoir des véhicules où tout est sacrifié à la légèreté et qui emportent sans peine cette quantité d’accumulateurs. Pour les voitures à transformer, c’est déjà un problème que d’y loger la quantité d’accumulateurs nécessaires.
Pour augmenter le rayon d’action, on peut envisager plusieurs combinaisons. Raisonnons sur une voiture de 1200kg dont 300kg d’accus :
1) Au bout du rayon d’action de la batterie, on la dépose, pour en prendre une autre ; le rayon d’action initial de 52 km devient naturellement 104 km.
2) On emporte 300 kg. d’accus supplémentaires, et on les fait marcher quand la première batterie est épuisée : la voiture se trouve alors alourdie de 300 kg. et le rayon d’action va être
$$$ 104 \frac{1200}{1500} = 83km$$$
3) On emporte 300kg d’accus supplémentaires dans la voiture et on les fait marcher en parallèle avec la première batterie. La situation s’améliore parce que la décharge de chaque batterie se fait en 4 h au lieu de se faire en 2h. Tenant compte de l’augmentation de capacité qui en résulte, on trouve que le rayon d’action remonte à 102 km., presque identique à celui du premier cas : l’augmentation de capacité pour une décharge plus lente compense à peu près le fait d’avoir à transporter un poids plus grand, au moins pour l’ordre de grandeur des temps de décharge considérés (2 h, et 4 h.).
Si l’on avait raisonné sur un temps de décharge plus court, on aurait trouvé un plus grand avantage dans la combinaison 3, et si on avait raisonné sur un temps de décharge plus long, on aurait trouvé une grande supériorité dans la combinaison 1. Il y a donc une sorte de proportion optimum pour le poids d’accumulateurs à disposer dans une voiture électrique, et cette proportion est de l’ordre de 1/4 ou de 1/3. Il est préférable de ne pas trop s’en éloigner.
Pour compléter le bilan des poids, dans le cas d’une voiture à essence transformée, il faut encore tenir compte de tout ce qu’on enlève : moteur à essence, radiateur, réservoir à essence, etc. et du moteur électrique, en général notablement plus léger, que l’on y installe. En général, par rapport à ce qu’elle était au paravent, la voiture reste alourdie de 15 à 25 %.
Couple fourni par le moteur électrique
Soit un moteur électrique continu, avec un champ H dans l’entrefer, une vitesse angulaire ω, voyant passer dans son induit un courant i, alimenté par une tension de batteries E, avec une résistance totale r dans le circuit induit. Le moteur Fournit un couple AHi, A étant un coefficient de proportionnalité, et il présente une force électromotrice AHω, A étant le même coefficient.
Son régime de marche résulte donc des deux équations :
| (1) | E-AHω=ri |
| AHi=C (couple résistant) |
L’élimination de i permet de connaître la vitesse prise par la voiture (vitesse proportionnelle à ω) quand le couple C varie.
Nous allons voir comment les divers types de moteurs s’appliquent à la traction, en considérant d’abord le cas de moteurs marchant sans aucun réglage, puis celui de moteurs où l’on fait varier soit l’excitation H, soit la résistance r en série.
Nous admettrons que dans le régime normal la vitesse est ωo, le champ Ho, le courant io, le couple Co, et que, dans ce régime, rio représente 15% de la tension E. Les deux équations (1) s’écrivent alors :
| (2) | $$$ 1 - 0,85 \frac{H}{H_o}\frac{\omega}{\omega_o}=0,15 \frac{i}{{i}_o}$$$ |
| $$$ \frac{C}{C_o} = \frac{H}{H_o} \frac{i}{{i}_o}$$$ |
Considérons d’abord un moteur à excitation complètement indépendante qui sera toujours maintenue à la valeur $$$ \frac{H}{H_o} =1$$$. Nous aurons pour un tel moteur $$$ \frac{C}{C_o} = \frac{i}{{i}_o}$$$
et par conséquent $$$ 1 - 0,85\frac{\omega}{\omega_o}=0,15 \frac{i}{{i}_o}$$$
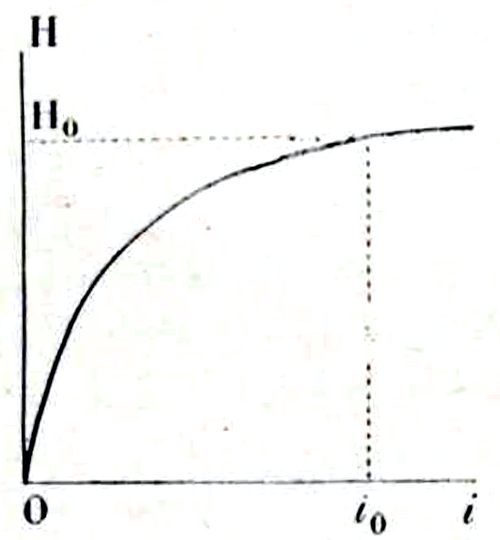
Considérons ensuite un moteur série, où l’excitation H dépend du courant i par une courbe qui a l’allure ; d’une courbe d’aimantation (cf. la figure). L’expérience montre qu’on la représente assez bien au moins dans sa partie utile, en admettant la relation
$$$ \frac{H}{H_o} = \sqrt{\frac{i}{i_o}}$$$
Adoptant cette valeur pour H, nous avons
(3) $$$ \frac{C}{C_o} = {\frac{i}{i_o}^{\frac{3}{2}}$$$
et, en éliminant dans l’équation des f. e. m. :
$$$ 1 - 0,85 {\frac{C}{C_o}}^{\frac{1}{3}} \frac{\omega}{\omega_o}=0,15 {\frac{i}{i_o}^{\frac{3}{2}}$$$
soit :
$$$ \frac{\omega}{\omega_o}= \frac{1 - 0,15 {\frac{C_o}{C}}^{\frac{2}{3}}}{0,85 {\frac{C}{C_o}}^{\frac{1}{3}}$$$
Le tableau suivant donne les conditions de vitesse réalisée et de puissance dépensée W pour nos deux moteurs, en fonction de $$$ \frac{C}{C_o}$$$
| Moteur série | < | Moteur H=cte | < | |
| $$$ \frac{C}{C_o}$$$ | $$$ \frac{\omega}{\omega_o}$$$ | $$$ \frac{W}{W_o}$$$ | $$$ \frac{\omega}{\omega_o}$$$ | $$$ \frac{W}{W_o}$$$ |
| 0,25 | 1,79 | 0,397 | 1,13 | 0,25 |
| 0,5 | 1,34 | 0,629 | 1,087 | 0,5 |
| 0,75 | 1,23 | 0,837 | 1,043 | 0,75 |
| 1 | 1 | 1 | 1 | 1 |
| 1,5 | 0,823 | 1,31 | 0,911 | 1,5 |
| 2 | 0,71 | 1,585 | 0,822 | 2 |
| 4 | 0,462 | 2,52 | 0,47 | 4 |
| 8 | 0,02 | 6.38 | <0 | 8 |
Voici donc les résultats que l’on peut attendre pour une voiture qui n’a ni changement de vitesse ni réglage électrique d’aucune sorte. On voit que le moteur à excitation constante conserve mieux la vitesse, mais au prix de plus grandes variations de puissance à demander à la batterie. Le moteur série, au prix d’une légère perte de vitesse par rapport au premier, est sensiblement moins exigeant dans les côtes.
Cependant, nous avons délibérément avantagé le moteur série sur deux points : l’allure parabolique de la courbe H, i ne se maintient pas, en fait, pour de grandes valeurs de i, à cause de la saturation, et les performances d’un moteur série pour des couples élevés ne peuvent être meilleures que celles d’un moteur complètement saturé. De plus, pour produire l’excitation du moteur série, il faut admettre une petite perte Joule supplémentaire, se traduisant par une chute de tension proportionnelle à i, et que nous avons négligée, La comparaison donnée dans le tableau ci-dessus est donc légèrement trop favorable pour le moteur série.
Pour préciser la signification des chiffres donnés ci-dessus, examinons à quoi correspond le cas où l’on a par exemple $$$ \frac{C}{C_o}= 4$$$
Si la voiture fait normalement du 35 km/h en palier, Co correspond à un frottement de 2%, Donc C correspond à 8%, soit 1,5% pour le frottement palier, et le reste pour monter une côte de 6,5%, la résistance de l’air étant négligeable puisqu’on va monter la côte lentement.
On voit que pour monter cette côte de 6,5 %, le moteur série fait un appel de puissance de 2,52 pour fournir la vitesse 0,46, tandis que le moteur à excitation constante fait un appel de puissance de 4 pour fournir la vitesse pratiquement identique de 0,47. Le moteur série parait donc nettement supérieur. Mais il ne faut pas oublier que nous l’avons pris assez peu saturé pour que la loi $$$ H \rho \sqrt{i}$$$ soit valable même pour les fortes intensités.
Si nous envisageons des côtes plus fortes, nous sommes très vite limités en arrivant à des intensités telles que E = r i, ne laissant plus rien pour la force contre-électromotrice du moteur lequel fournissant un couple insuffisant, ne peut plus entraîner la voiture.
Les changements de vitesses électriques et mécaniques
Pour remédier à cette situation, nous pouvons, soit utiliser un changement de vitesse mécanique, qui nous oblige à disposer également sur la voiture un embrayage.
Si par exemple nous introduisons un changement de vitesse rapport 1/2 pour une même vitesse du moteur, nous doublons le couple en divisant par deux la vitesse de la voiture, d’où les nombres du tableau suivant (ω se rapportant à la vitesse de la voiture) :
| Moteur série | < | Moteur H constant | < | |
| $$$ \frac{C}{C_o}$$$ | $$$ \frac{\omega}{\omega_o}$$$ | $$$ \frac{W}{W_o}$$$ | $$$ \frac{\omega}{\omega_o}$$$ | $$$ \frac{W}{W_o}$$$ |
| 0,5 | 0,9 | 0,397 | 0,56 | 0,25 |
| 1,5 | 0,615 | 0,827 | 0,2 | 0,75 |
| 1 | 0,67 | 0,629 | 0,543 | 0,5 |
| 2 | 0,5 | 1 | 0,5 | 1 |
| 3 | 0,4 | 1,31 | O,455 | 1,5 |
| 4 | 0,355 | 1,585 | 0,411 | 2 |
| 8 | 0,231 | 2,52 | 0,235 | 4 |
| 16 | 0,01 | 6,28 | <0 |
Mais le changement de vitesse introduit un léger rendement, dont il faut tenir compte, et qui vient majorer un peu les puissances précédentes.
On peut arriver à des résultats équivalents avec ce que nous appellerons un changement de vitesse électrique.
Dans un moteur à essence, le couple est limité par la force de l’explosion dans chaque cylindre, et la puissance est proportionnelle à la vitesse de rotation (en gros). Dans un moteur électrique, la puissance croit sans limite avec l’intensité. Une forte surcharge pendant un certain temps permet d’augmenter beaucoup la puissance sans prendre aucune disposition spéciale. Ce qui, en pratique, limite l’intensité qui traverse l’induit, c’est l’existence de la force contre-électromotrice.
Revenons alors aux équations (1). supposons que nous divisions nos batteries en deux groupes que nous mettrons en parallèle : la tension E devient E/2, la vitesse ω ne peut dépasser la valeur ω1, telle que AHω1=E/2, vitesse voisine de la moitié de la vitesse de régime normale. Si à ce moment les circonstances de la route sont telles que l’intensité se règle à une valeur élevée, nous pourrons effectivement la fournir en fatiguant deux fois moins les batteries, résultat obtenu en consentant à marcher à peu près deux fois moins vite.
Nous avons encore une autre ressource, qui est de varier le coefficient A ; supposons que notre moteur ait deux induits, mis en parallèle pour la marche normale ; à ce moment, ils sont chacun traversé par le courant i, et le coefficient du couple pour chacun est A, tel que $$$ C = AH (\frac{i}{2}+\frac{i}{2})$$$
Mettons ces deux induits en série, le même courant i les traverse cette fois tous les deux, donc C = 2AHi.
En acceptant par conséquent de fatiguer le moteur (qui le supporte très bien), nous obtenons ici un couple double pour le même courant demandé aux batteries, en doublant, il est vrai, la force contre-électromotrice qui devient 2AHω, ce qui limite, comme plus haut, à une valeur moitié la vitesse que la voiture peut atteindre,
Notons enfin qu’on obtient la marche arrière en inversant le sens du courant dans l’induit ou le sens du champ par l’inversion des inducteurs.
Mais la résistance r a aussi varié dans l’opération de mise en série parallèle, ceci introduit également un rendement tout comme dans un changement de vitesse mécanique.
A quelle combinaison, mécanique ou électrique, doit-on donner la préférence ? c’est selon. Le changement de vitesse mécanique (auquel il faut ajouter l’embrayage) a contre lui sa complication et son prix. Il a pour lui l’avantage d’exister sur les voitures à transformer ; si on l’adopte, il simplifie beaucoup le schéma électrique, il permet notamment des démarrages à vide du moteur débrayé sans aucune résistance de protection. Enfin, le rendement qu’il introduit est constant et élevé, alors que le rendement du changement de vitesse électrique, dans les combinaisons donnant de forts couples et de basses vitesses, décroît terriblement vite quand l’intensité croit.
Le changement de vitesse électrique a le grand avantage d’une réalisation facile, mais sur les voitures où la puissance des batteries et du moteur a été très mesurée, la baisse de rendement qu’il occasionne aux régimes à fortes intensités le rend peu désirable la plupart du temps. A méthodes de fabrication comparables, il serait certainement moins cher qu’un changement de vitesse mécanique, mais, en fait, pour des voitures à transformer, il est rare qu’il se présente d’une manière intéressante.
Moyens de réglage de la vitesse
En dehors du changement de vitesse proprement dit, qui opère par variation brusque, il reste intéressant de pouvoir régler la vitesse d’une voiture électrique à la manière de ce qu’on obtient avec une voiture à essence en appuyant sur l’accélérateur.
Dans le cas du moteur série, nous pouvons par exemple insérer une résistance réglable R en série. Mais si nous nous reportons aux équations (1) et (2) nous voyons que l’intensité i qui passe est déjà entièrement déterminé par le couple résistant. Il en résulte que la résistance R en série ne fera que diminuer la f.e.m. agissante qui de E va devenir E-Ri, en diminuant la vitesse de la voiture, mais sans la moindre économie de puissance, puisque le point Ei ne change pas. C’est une faiblesse assez sérieuse du moteur série, avec ou sans changement de vitesse.
Dans le cas du moteur à excitation indépendante, nous pouvons régler plus on moins l’excitation, à une valeur αH an lieu de H. On trouve alors que s’il y a un changement de vitesse, on peut avoir intérêt, pour réaliser une économie de puissance, à se placer à un régime qui donnerait, à excitation maximum, un excès de couple, et à réduire ce couple par diminution de l’excitation, pour l’adapter à celui que demande la route.
En reprenant l’exemple que nous avons pris plus haut, et en remplaçant H par αH, nous avons :
$$$ \frac{i}{i_o} = \frac{1}{\alpha} \frac{C}{C_o}$$$
et : $$$ 1 - 0,85 \alpha \frac{\omega}{\omega_o} = \frac{0,15}{\alpha} \frac{C}{C_o}$$$
d’où :
$$$ \frac{\omega}{\omega_o} = \frac{1,175}{\alpha} - \frac{0,175}{\alpha^2}\frac{C}{C_o}$$$
Reprenons le cas typique de C/Co = 4, qui représente une côte de 6%. Nous savons déjà qu’on peut la monter :
en moteur série :
en prise, à 0,46 V, avec puissance 2,5 ;
avec changement de vitesse 1/2, à O,355 V, avec puissance 1,55 ;
en moteur indépendant :
en prise α= 1 à 0,47 V, avec puissance 4 ;
avec rapport 1/2 α= 1, à 0,411 V, avec puissance 2.
Mais nous pouvons aussi, en donnant par exemple à α la valeur 0,75 la monter :
en prise, à 0,315 V, avec puissance 5,3 ;
avec rapport 1/2, à 0,47 V, avec puissance 2,66.
Comme la puissance d’excitation d’un moteur bien construit est négligeable (1 à 3 % de la puissance nominale), nous n’avons pas à la faire entrer en ligne de compte, et nous pouvons conclure qu’un moteur à excitation indépendante, bien conduit, donnera au moins les mêmes résultats qu’un moteur série.
Si l’on risque au contraire de mal conduire, le moteur série gardera des avantages pour la sécurité.
Mais il y a un gros argument en faveur du moteur à excitation indépendante : il permet la récupération dans les descentes, en freinant en même temps la voiture : en effet, le sens du champ dans le moteur est invariable ; si l’induit tourne plus vite, la force contre-électromotrice du moteur devenant supérieure à la tension de la batterie, on débite un courant de charge dans celle-ci, circonstance qui ne se produit pas dans le cas d’un moteur série. L’expérience montre que ce freinage est extrêmement intense et l’on est conduit plutôt à désexciter la voiture pour la laisser un peu rouler.
Dans le cas d’une récupération bien conduite, dans la traction électrique sur voie ferrée par exemple, on arrive à récupérer ainsi 30 % de l’énergie sur un trajet donné, nous n’avons pas de chiffres à citer dans le cas de la traction sur route, il est probable que le gain de rayon d’action dû à la récupération reste très intéressant, si on ne l’a pas payé par trop d’« écarts de conduite » consommant du courant,
Emploi du moteur compound
En pratique, le moteur compound, avec forte prépondérance de l’excitation shunt, paraît remporter la majorité des suffrages. Voici comment se justifie cette forte prépondérance du shunt : si, à un instant donné, sur la voiture en marche, on diminue l’excitation shunt, diminuant la f.c.e.m., on provoque un appel de courant dans l’induit. Mais ce courant d’induit, augmenté, augmente l’excitation grâce à l’inducteur série, il y a donc une sorte d’effet de contre-réaction qui fait que, si l’on veut avoir une action de réglage sur le champ, l’excitation doit être presque entièrement shunt.
Voici comment on peut chiffrer cet effet.
Le champ H est Fonction des ampères.tours. Ceux-ci ont un terme $$$ H^2 + (1-A)\frac{1 - (1-\epsilon)H\omega}{\epsilon} H\omega = \frac{1 - A}{\epsilon} + Ai $ </math> En supposant ε=0,1, soit un très beau rendement, et en faisant A=O,75, soit une prépondérance déjà marquée du shunt, on a en fonction des vitesses ω la valeur de {i}, pour obtenir les champs H, donnée par le tableau suivant: $$$0||||
On règle alors la vitesse en donnant l’excitation shunt au moteur, mais ceci n’a naturellement d’intérêt que si l’on a un excès de couple à sa disposition, le réglage de la vitesse consistant uniquement à diminuer H en diminuant le couple AHi pour augmenter ω en maintenant la force contre-électromotrice AHω voisine de la tension d’alimentation E.
Les leçons de la pratique
Comme nous l’avons dit, la puissance, calculée pour un roulement à certains étals de régime, ne donne aucune idée des besoins pratiques en couple de la voiture, pour obéir aux conditions de la conduite en ville : accélérer pour dépasser un obstacle, pour franchir un croisement, pour obéir à un signal d’agent, etc...
D’après des essais faits sur une petite voiture transformée, pesant en charge 7OOkg, il semble qu’il soit agréable de pouvoir dépenser de temps en temps 3 CV (compte tenu de tous les rendements : moteur, transmission, etc...), il faudrait donc que l’on dispose dune puissance permanente de 735 x 3 = 2 205 watts, et, si l’on veut marcher pendant 2 heures, il faudrait donc emmagasiner 44OO Wh à un régime de 2 heures. Si l’on se donne 23 Wh par kg d’accumulateur à cette vitesse de décharge, on est conduit à 200 kg de batterie. On a donc, comme rapport du poids de la batterie au poids de la voiture :
λ = 200 / 700 = 0,286
ce qui nous amène à prévoir un rayon d’action de 58 km environ, d’après le tableau des rayons d’action précédemment donné, assez d’accord par conséquent avec le chiffre pratique de 62 km obtenu. Par conséquent, nous obtenons là d’une autre manière, en partant en quelque sorte de la puissance qui commence à donner quelques satisfactions de conduite, une évaluation qui concorde avec les autres.
Bien entendu, il s’agit ici de parcours en ville, et même dans une ville à relief peu accentué, comme Paris. En fait, la voiture électrique obtient ses plus grands triomphes dans les villes très plates, comme Lyon (La Croix-Rousse exceptée). À la campagne, on pourrait songer aussi à la répandre dans des pays de plaine, mais il ne faudrait pas qu’on puisse se mettre à dire : « il fait un vent à ne pas mettre une voiture électrique dehors ». Nous voulons rappeler par là que la voiture électrique devra être soigneusement profilée, au point de vue aérodynamique, pour tirer le maximum de ses possibilités.
Rappelons-le encore : des arrêts et des démarrages fréquents augmentent les possibilités, fie sorte que finalement la voiture électrique jouit des qualités demandées pour le service de ville, où elle donne une vitesse moyenne, compte tenu des arrêts aux barrages et carrefours bien voisine de celle des voitures à essence.
Nous discuterons dans un prochain article le très délicat problème de la recharge des accumulateurs.
(manuscrit reçu le 25 novembre 1940)


