Résumé :

Reçu le 28 octobre 2020Accepté le 7 juin 2021 DOI :https://doi.org/10.1103/PhysRevLett.127.081602

Publié par l’American Physical Society selon les termes de la licence Creative Commons Attribution 4.0 International. Toute distribution ultérieure de ce travail doit maintenir l’attribution à l’auteur ou aux auteurs et le titre de l’article publié, la citation du journal et le DOI. Financé par SCOAP3.

Auteurs & affiliations

Maulik Parikh1,2, Frank Wilczek1,3,4,5, et George Zahariade1,2

1. Département de physique, Arizona State University, Tempe, Arizona 85287, USA
2. Beyond Center for Fundamental Concepts in Science, Arizona State University, Tempe, Arizona 85287, USA
3. Département de physique, Université de Stockholm, Stockholm SE-106 91, Suède
4. Center for Theoretical Physics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA
5. Wilczek Quantum Center et T. D. Lee Institute, Shanghai 200240, Chine

Introduction

Le comportement des objets en chute libre sous l’influence de la gravité est généralement décrit par la théorie générale de la relativité d’Einstein, le champ de courbure étant traité de manière classique. Les particules test individuelles suivent l’équation géodésique tandis que les séparations de paires de particules test obéissent à l’équation de déviation géodésique. Ce sont des équations déterministes, qui conviennent à la théorie classique dont elles sont dérivées. Mais les lois fondamentales de la physique relèvent de la mécanique quantique et, dans le contexte de la gravité, nous nous attendons à ce que la métrique de l’espace-temps soit un champ quantique. Pour en tenir compte, un cadre différent est nécessaire.

Nous présentons ici un formalisme permettant de calculer l’effet sur la chute des corps dû à la quantification du champ gravitationnel. Nous constatons que la dynamique de la séparation d’une paire de particules en chute n’est plus déterministe, mais probabiliste, et qu’elle est influencée par une nouvelle force stochastique. Plus précisément, nous constatons que la séparation des deux particules obéit maintenant à une équation stochastique de type Langevin contenant un terme de fluctuation aléatoire, ou bruit [1] (comme cela est discuté plus en détail dans le matériel supplémentaire [2] et plus complètement dans la Réf. [3]). Ceci fournit la généralisation quantique de l’équation classique de déviation géodésique. Notre résultat s’applique également à un objet unique tombant dans le champ gravitationnel d’une masse fixe plus lourde. Ainsi, une pomme tombant dans le champ gravitationnel de la Terre, par exemple, ne tomberait pas directement vers le bas mais serait soumise à de minuscules secousses quantiques, que l’on peut considérer de manière heuristique comme dues au bombardement de la pomme par des gravitons.

Cet effet est potentiellement mesurable par les détecteurs d’ondes gravitationnelles. Nous pouvons modéliser les miroirs d’un bras d’un interféromètre à ondes gravitationnelles [4] [5] comme deux particules en chute libre, et les coupler à un champ gravitationnel faible quantifié. Ensuite, en utilisant notre formalisme (qui est basé sur la fonction d’influence de Feynman-Vernon), l’effet sur la séparation des miroirs peut être calculé ; le résultat est que la séparation des miroirs est soumise à un bruit quantique-gravitationnel. De plus, le spectre de puissance inhabituel de ce bruit peut permettre de le distinguer de nombreuses autres sources de bruit auxquelles les interféromètres à ondes gravitationnelles sont sensibles [6]. Les propriétés statistiques du bruit dépendent de l’état quantique du champ gravitationnel, et nous l’avons calculé explicitement pour plusieurs classes d’états. Nous estimons que le bruit est infiniment petit pour les états cohérents, qui sont des états quantiques à incertitude minimale qui ressemblent le plus aux ondes gravitationnelles classiques. Cependant, il existe des phénomènes théoriquement prédits, mais encore non observés, impliquant l’évaporation des trous noirs et des phases exotiques dans l’univers primitif, dans lesquels les aspects quantiques du rayonnement gravitationnel jouent un rôle central. Pour les états quantiques correspondants, nous constatons que le bruit peut être considérablement accru. En particulier, dans les états comprimés, le bruit peut être augmenté de façon exponentielle par le paramètre de compression. La détection de ce bruit fondamental fournirait une preuve expérimentale de la quantification de la gravité. Enfin, nous discutons également du lien entre les caractéristiques des sources de rayonnement et la nature quantique du champ de rayonnement.

Analyse

Nous nous intéressons à la façon dont une paire de particules en chute libre répond à un champ gravitationnel quantifié (voir Réf.  [7]  [8]  [9]  [10]  [11]  [12]). Nous appelons cette paire un détecteur car les deux miroirs situés aux extrémités du bras d’un interféromètre à ondes gravitationnelles peuvent être idéalisés comme deux particules massives en chute libre dans un champ gravitationnel faible. (Cette description serait plus littéralement valable pour un interféromètre spatial). Supposons que l’état initial du champ gravitationnel soit le suivant |Ψ⟩ . Nous avons à l’esprit que cet état initial a été créé par des sources astrophysiques lointaines et peut donc être considéré comme initialement non enchevêtré avec l’état du détecteur. Lorsque le champ interagit avec le détecteur, son état quantique change parce que le détecteur absorbe et émet génériquement des gravitons par émission spontanée et stimulée ; l’état final du champ |f⟩ est a priori inconnu. Nous aimerions connaître la probabilité de transition pour que le détecteur passe de l’état |A⟩ à l’état |B⟩ dans le temps T. Puisque nous ne mesurons pas l’état final du champ gravitationnel, nous devons faire la somme des éléments suivants |f⟩. Ainsi, nous souhaitons calculer

(1)

où |a,b⟩≡|a⟩⊗|b⟩ et Û est l’opérateur unitaire d’évolution temporelle pour le champ gravitationnel combiné + système détecteur.

Pour aller plus loin, nous avons besoin d’une description plus détaillée des degrés de liberté observés ; il est important de se concentrer sur les observables car les variables naturelles comprennent une dépendance de jauge non physique. Supposons que la séparation géodésique des deux particules est de ξ(t). La dynamique du système combiné de la gravité et des deux particules est décrite par l’action d’Einstein-Hilbert minimalement couplée aux actions des deux particules non relativistes. La faiblesse du champ gravitationnel dans les zones de radiation nous permet de développer l’interaction particule-champ, qui est notre intérêt principal, dans la perturbation métrique h_ij. Nous conserverons également jusqu’à des termes quadratiques dans l’action purement gravitationnelle. Cette troncature néglige l’auto-interaction gravitationnelle. Elle correspond à la sommation d’une grande classe de graphes de Feynman, comme indiqué sur la figure 1. Alors,

(2)

Dans cette expression, il ne nous reste qu’un seul degré de liberté pour les deux particules : leur séparation invariante de jauge. Ainsi, nos résultats s’appliquent également au cas d’une particule unique soumise à la gravité d’une masse fixe plus lourde. Nous pouvons maintenant évaluer les amplitudes dans l’équation (1) dans la formulation de l’intégrale du chemin dérivée de l’action dans l’équation (2), où |A⟩ et |B⟩ sont les états initial et final de ξ ; voir Fig. 1. Ainsi, nous avons

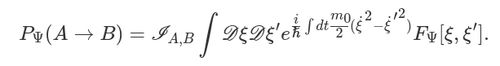
(3)

Cette expression peut être comprise comme suit. L’intégrale du double chemin traduit le fait qu’il s’agit d’une probabilité, plutôt que d’une amplitude. Le facteur I _A,B contient des intégrales sur les fonctions d’onde initiales et finales de ξ et ne jouera aucun autre rôle. Dans l’exposant, nous reconnaissons l’action non relativiste pour une particule libre. L’équation (3) nous donne une théorie effective pour la séparation des particules ξ dans laquelle les effets de son couplage avec le champ gravitationnel quantifié ont été pris en compte. De façon cruciale, tous les effets du champ gravitationnel quantifié sont formellement capturés par la fonction F_Ψ[ξ,ξ′] connue sous le nom de fonction d’influence de Feynman-Vernon [13]  [14]  [15].

Pour évaluer la fonction d’influence, nous écrivons l’état du champ gravitationnel $$$ \vert \Psi \rangle$$$ comme un produit tensoriel d’états monomodes : $$$ \vert \Psi \rangle = \bigotimes_{\vec{k}} \vert \Psi_{\vec{k}} \rangle$$$. Pour un champ gravitationnel faible, la linéarité nous permet de traiter le problème mode par mode puis de faire la somme sur les modes. Alors , $$$ F_{\Psi} [ \xi , \xi′ ] = \Pi_{\vec{k}} F_{\Psi_{\vec{k}}}[ \xi , \xi′ ]$$$ où $$$ F_{\Psi_{\vec{k}}}[ \xi , \xi′ ]$$$ est la fonction d’influence pour un seul mode du champ gravitationnel. Pour la calculer, nous décomposons la perturbation métrique en modes de Fourier. Soit le mode de nombre d’onde $$$ \vec{k}$$$ a une fréquence angulaire $$$ \omega_\vec{k}$$$ et une amplitude $$$ q_\vec{k} (t)$$$. Si nous supposons maintenant, pour simplifier, que la perturbation se propage orthogonalement à la ligne joignant les particules, et si nous nous limitons à une seule polarisation, nous trouvons que la partie gravitationnelle de l’action de l’équation (2) pour un seul mode du champ gravitationnel est

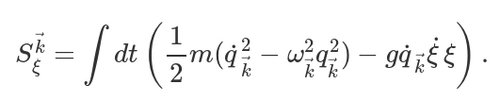
(4)

Ici, $$$ g= \frac{m_0}{2 \sqrt{\frac{\hslash G }{c^3}}}$$$ est une constante de couplage, tandis que m est une masse introduite pour des raisons dimensionnelles ; m dépend d’une échelle de coupure infrarouge et disparaît de toutes les expressions physiques après intégration sur les modes.

Le modèle peut être rendu plus réaliste en incluant l’autre polarisation, ainsi qu’en tenant compte de divers facteurs trigonométriques qui surviendraient pour des modes incidents depuis des directions différentes ; nous négligeons ici ces raffinements compliqués pour nous concentrer sur le problème central.

Remarquez que l’action monomodale de l’équation (4) décrit un simple oscillateur harmonique de fréquence angulaire $$$ \omega_\vec{k}$$$ couplé à une source externe ξ, via une interaction cubique et dérivée. Nous pouvons facilement quantifier cette action simple pour évaluer la fonction d’influence ; le calcul peut être effectué, sans invoquer davantage la théorie des perturbations, car le Lagrangien est quadratique en q. L’hamiltonien quantique associé se lit comme suit $$$ \hat{H}^{\vec{k}}_{\xi} = \frac{ (\hat{p}_{\vec{k}} + g \xi {\dot{\xi}} )^2}{2m} + \frac{1}{2} m {\omega_\vec{k}}^2 {\hat{q}_{\omega_\vec{k}}}^2$$$. Corrélativement, l’expression de la fonction d’influence monomodale est la suivante $$$ F_{\Psi_{\vec{k}}} [ \xi , \xi'] = \langle \Psi_{\vec{k}} \vert {\hat{U}_{\xi'}}^{\vec{k}\dagger} (T) {\hat{U}_{\xi'}}^{\vec{k}} (U) \vert \Psi_{\vec{k}} \rangle$$$ où $$$ {\hat{U}_{\xi'}}^{\vec{k}}$$$ est l’opérateur unitaire d’évolution temporelle obtenu à partir de $$$ {\hat{H}_{\xi'}}^{\vec{k}}$$$. L’application répétée de la formule de Baker-Campbell-Hausdorff permet alors d’obtenir

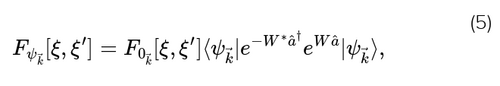
où W et $$$ F_{0_{\vec{k}}} [ \xi , \xi']$$$ sont des fonctions facilement calculées de ξ et ξ′. L’équation (5) est utile sur le plan du calcul car les exposants sont exprimés en termes d’opérateurs d’échelle â et â^†, dont l’opération sur $$$ \vert Psi_{\vec{k}} \rangle$$$ peut être calculé pour de nombreuses classes d’états. En particulier, Eq. (5) peut être évaluée en forme fermée pour les états de vide, cohérents, thermiques et comprimés.

Après avoir obtenu la fonctionnelle d’influence pour un seul mode du champ gravitationnel dans un état initial $$$ \vert Psi_{\vec{k}} \rangle$$$, nous sommes maintenant prêts à faire la somme des modes pour trouver la fonctionnelle d’influence totale du champ gravitationnel à partir du produit des fonctionnelles d’influence monomodes. Le résultat dépendra de l’état quantique du champ gravitationnel. Comme exemple de base, supposons que le champ gravitationnel soit dans son état de vide. En effectuant la somme des modes, nous trouvons en particulier que

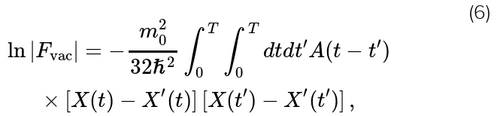
où $$$ X =d^2 (\xi^2)/dt^2$$$, $$$ X' =d^2 (\xi'^2)/dt^2$$$ et A(t - t′) est une intégrale connue. Feynman et Vernon ont réalisé que lorsque ln|F| est quadratique en X-X′, |F| peut être réécrite de manière très suggestive, comme une moyenne statistique sur une fonction auxiliaire N(t) :

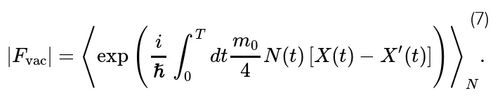
Ici, la fonction N(t) obéit à une distribution de probabilité gaussienne avec une fonction d’autocorrélation stationnaire A(t - t′). Ainsi, l’effet du couplage au vide quantique-gravitationnel, qui est entièrement codé en F_vac, est d’introduire un bruit stochastique stationnaire dans le détecteur. Comme nous allons le voir, cela crée des fluctuations dans la longueur du bras. Toutes les propriétés statistiques de ces fluctuations, comme l’écart-type, peuvent être obtenues à partir de la fonction d’autocorrélation, A(t - t′). En revanche, on constate que la phase de F_vac a une structure différente, qui est responsable des effets dissipatifs. Pour un état cohérent correspondant à une onde gravitationnelle classique h(t) la phase de la fonction d’influence contient également un terme $$$ \frac{i}{\hslash} \int_@ ^T (1/4)m_0 h(t) [X(t) - X′(t)]$$$.

Déviation géodésique quantique

Jusqu’à présent, nous nous sommes concentrés sur la fonctionnelle d’influence de Feynman-Vernon pour un détecteur couplé à un champ gravitationnel, en traitant à la fois le détecteur et le champ de façon mécanique quantique. Puisque les détecteurs réalistes sont bien approximés comme classiques, il est approprié d’exploiter cette simplification. Dans notre expression pour la probabilité de transition, Eq. (3), nous identifions les chemins classiques, qui dominent l’intégrale, comme ceux qui rendent les phases stationnaires. Cela conduit à une équation de mouvement stochastique effective pour la séparation des masses ou, de manière équivalente, pour la longueur du bras d’un détecteur d’ondes gravitationnelles. En présence d’une onde gravitationnelle classique h(t), on trouve

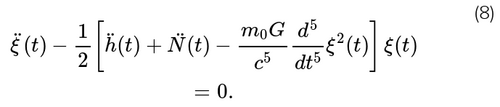
Ainsi, l’accélération relative des deux masses $$$ \ddot{\xi}$$$ dépend de trois termes. Chaque terme de cette équation, qui étend l’équation de déviation géodésique de la relativité générale au cas où la métrique de l’espace-temps est traitée comme un champ quantique, a une signification intuitive. Le premier représente l’accélération de marée habituelle due au passage d’une onde gravitationnelle classique h ; c’est l’effet qui a été mesuré de façon célèbre par LIGO. Le dernier terme est la contrepartie gravitationnelle du terme dissipatif d’Abraham-Lorentz en électromagnétisme ; il s’agit de la réaction de rayonnement gravitationnel [16]  [17]  [18]  [19]. Bien qu’il soit susceptible d’avoir peu de conséquences expérimentales, il est néanmoins remarquable qu’un tel terme apparaisse dans une théorie quantique bien conduite. (Comme nous le signalerons ailleurs, cette approche de la réaction de rayonnement évite les pathologies notoires qui découlent d’une interprétation trop littérale de l’équation d’Abraham-Lorentz [20]). Plus important encore, notre équation contient un terme de bruit $$$ \ddot{N}$$$. Ainsi, notre équation, bien que classique, est stochastique plutôt que déterministe [14,15]. Elle rappelle, sur le plan mathématique, l’équation de Langevin utilisée pour décrire le mouvement brownien.

Nous avons calculé les propriétés statistiques de ce bruit, plus précisément le spectre de puissance S(ω), dans plusieurs cas ; un calcul précis du spectre de puissance quantique-gravitationnel est essentiel pour distinguer le bruit d’autres sources de bruit moins fondamentales dans les détecteurs d’ondes gravitationnelles [21] [22]. S est la transformée de Fourier de la fonction d’autocorrélation A(t - t′). Pour le vide et pour les états cohérents, on trouve que, pour les basses fréquences, le spectre de puissance se comporte comme $$$ S = 4G \hslash \omega /c^5$$$. Pour les états thermiques à la température T, on trouve $$$ S = 4G \hslash \omega /c^5 coth (\hslash \omega / ak_B T)$$$. Il est frappant de constater que si le champ gravitationnel est dans un état comprimé avec le paramètre de compression r, nous constatons que le bruit contient également une partie non stationnaire ; en se concentrant sur la partie stationnaire, nous trouvons $$$ S= \sqrt{cosh 2r} 4G \hslash \omega /c^5$$$, ce qui signifie que les fluctuations induites par les quanta de la longueur du bras du détecteur peuvent être renforcées de manière exponentielle.

Discussion

Nous avons montré qu’une paire de particules en chute libre dans un champ gravitationnel quantifié obéit à l’équation stochastique (8), plutôt qu’à l’équation classique de déviation géodésique ; voir Fig. 2. Estimons la taille des fluctuations, en négligeant le terme de réaction de radiation. Alors , $$$ \xi(t) \approx [1 + (h + N ) / 2 ] \xi_0$$$, où ξ₀ est la longueur d’équilibre du bras ; pour LIGO, ξ₀ ≈ 4 km, tandis que pour LISA ξ 0₀ ≈ 10⁶ km. Comme le montre clairement la formule, les fluctuations de N induisent des fluctuations de ξ. On trouve que $$$ \langle \xi \rangle = ( 1 + h(t)/2)\xi_0$$$ avec une variance $$$ \sigma^2 = \xi^2 \langle N^2 \rangle /4 = \xi^2_0 A(0) /4$$$. Bien que $$$ A(0) = 1 /\pi \int_0^{\infty} d \omega S(\omega)$$$ est formellement divergent, la taille des fluctuations est néanmoins finie parce que les limites de la sensibilité du détecteur imposent une coupure ω_max sur l’intégrale de fréquence ; pour LIGO, ω_max∼1kHz tandis que pour LISA ω_max∼0,1Hz. Avec ces valeurs numériques, l’amplitude des fluctuations de l’état de vide σ∼l_Pξ₀ω_max/c est approximativement une longueur de Planck l_P et, par conséquent, totalement inobservable ; en fait, la même amplitude est également obtenue lorsque le champ gravitationnel est dans un état cohérent correspondant à une onde gravitationnelle classique se propageant dans le vide [9].

Cependant, l’amplitude des fluctuations peut être accrue pour les états non cohérents du champ gravitationnel. Comme exemples représentatifs, nous pouvons considérer des états formés par l’action d’opérateurs de déplacement représentant le champ classique h agissant non pas sur le vide, mais sur des états thermiques ou comprimés. Pour les états thermiques à la température T, nous avons constaté une augmentation d’un facteur $$$ \sqrt{2k_B T / \hslash \omega_max}$$$. De tels états thermiques pourraient apparaître, par exemple, à travers le fond isotrope d’ondes gravitationnelles cosmiques ( T∼1K) ou à la suite de l’évaporation de Hawking des trous noirs [23]. Dans ce dernier cas, la température peut être très élevée, mais il y a une suppression supplémentaire due à la localisation de la source. Plus prometteur encore, il peut y avoir un bruit important pour les états comprimés. Comme indiqué plus haut, nous nous attendons à ce que l’amplitude des fluctuations soit augmentée de façon exponentielle par le paramètre de compression $$$ \sigma \sim e^{r /2} l_P \xi_0 \omega_{max} /c$$$. Physiquement, les états comprimés gravitationnels peuvent avoir différentes origines possibles. Les vacuoles comprimées peuvent apparaître dans la cosmologie inflationniste [24]  [25]  [26] Mais en outre, les états comprimés sont naturellement produits par des sources classiques à travers les non-linéarités de la gravité, sans supposer une quelconque physique exotique.

En effet, il est éclairant de comparer la nature quantique des champs de rayonnement électromagnétique et gravitationnel pour des sources connues et envisagées ; le bruit quantique des photons sur la dynamique des particules chargées est analogue et fait bien sûr l’objet de l’optique quantique. Il est presque toujours approprié de traiter le couplage des champs électromagnétiques à leurs sources comme linéaire. Lorsqu’un champ de rayonnement est couplé linéairement à des degrés de liberté dynamiques qui sont décrits, avec une bonne approximation, comme déterministes et seulement faiblement perturbés par le rayonnement, alors le champ de rayonnement sera bien décrit par un état quantique cohérent [27]. C’est le cas pour la plupart des sources radio et micro-ondes et pour les lasers. Lorsque les sources elles-mêmes sont stochastiques, on obtient un mélange stochastique d’états cohérents. C’est le cas des sources les plus courantes (quasi-thermiques) à haute fréquence. Avec des techniques spéciales, par exemple en utilisant des cristaux non linéaires, on peut construire des sources dont le couplage au champ électromagnétique est quadratique, ce qui conduit à des états comprimés. Le traitement « classique » par défaut du rayonnement gravitationnel, qui correspond aux états cohérents, est approprié lorsque les sources sont régies par une dynamique approximativement déterministe impliquant un couplage linéaire faible au champ gravitationnel. Dans ce cas, en effet, on étend l’action quantique autour d’une solution classique des équations d’Einstein-Hilbert (incluant un espace-temps plat dans la zone de rayonnement). Il s’agit souvent d’un défaut approprié, par exemple pour décrire la décroissance orbitale lente de grands corps. Elle ne s’applique pas directement au rayonnement de Hawking, qui est un processus quantique quasi-thermique, ni à ses analogues cosmologiques ou, de manière plus spéculative, aux transitions de phase dans l’Univers primitif. Au cours des dernières étapes de la fusion des trous noirs, l’approximation consistant à traiter le rayonnement gravitationnel comme une perturbation linéaire faible n’est pas appropriée, malgré la nature déterministe de la dynamique. Dans ce cas, on peut s’attendre à rencontrer des effets que nous pourrions appeler le moulage de l’état de rayonnement quantique, qui vont au-delà de l’écrasement (quadratique).

Remerciements

Nous remercions Paul Davies, Bei-Lok Hu, Phil Mauskopf, Siddharth Morampudi, Igor Pikovski, et Tanmay Vachaspati pour leurs conversations. Au cours de ce travail, M. P. et G. Z. ont été soutenus en partie par la subvention n° 60253 de la Fondation John Templeton. G. Z. remercie également le Foundational Questions Institute et Moogsoft pour leur soutien. F. W. est soutenu en partie par le Département américain de l’énergie sous la subvention n° DE-SC0012567, par le Conseil européen de la recherche sous la subvention n° 742104, et par le Conseil suédois de la recherche sous le contrat n° 335-2014-7424.

Document complémentaire