Les auteurs anciens s’accordent à dire que l’art de l’arpentage prit naissance en Égypte où son emploi s’imposa dès que l’agriculture y fut en usage, à cause des débordements du Nil qui, chaque année, faisaient disparaître en partie les limites des propriétés.
Le plus ancien instrument dut être l’équerre d’arpenteur que les Égyptiens, et d’après eux les Grecs, appelaient l’astérique ou l’étoile ; les Romains la nommaient groma d’où est venu le terme gromaticus pour désigner un arpenteur. Elle se composait de deux tiges fixées à angle droit aux extrémités desquelles pendaient des fils à plomb ; le pied devait être disposé de manière à ne point gêner les visées.

Il démontre en effet que les deux plans ne seront perpendiculaires entre eux qu’autant que l’astérique sera horizontale, l’angle droit tracé sur l’astérique n’étant la mesure de l’angle dièdre formé par les plans verticaux qu’autant qu’il se trouve dans un plan qui leur est perpendiculaire.
Les ingénieurs avaient donc cherché un instrument plus parfait [2] ; Héron dit qu’il existait de son temps une foule de dispositions différentes, mais qui toutes laissaient à désirer, parce qu’elles me donnaient la solution que d’un petit nombre de problèmes. Nous ignorons complètement aujourd’hui en quoi elles pouvaient consister ; heureusement il nous est resté la description de l’appareil inventé par Héron sous le nom de Dioptre et qui fut certainement le plus parfait de tous.
Il n’est point sans intérêt de le faire connaître, ne fût-ce que pour montrer comment les anciens entendaient la construction d’un appareil de précision. C’est du reste le seul exemple d’appareil de ce genre dont la connaissance soit parvenue jusqu’à nous.
La traduction suivante du texte de l’ingénieur byzantin est due à M. Vincent, de l’Institut ; elle a été publiée en 1858 dans les Mémoires de l’Académie des Inscriptions et Belles-Lettres. La figure 2 représente la restitution qu’a proposée ce savant [3].
Soit donc AB le plateau qui environne l’axe et qui est attaché d’une manière fixe au support ; ΓΔ la roue dentée qui fait corps avec le tube ; EZ la vilt placée à côté de cette roue ; HΘ le tube adhérent à la roue, qui porte, comme on l’a dit, un chapiteau dorique KΛ. Maintenant, sur la plinthe de ce chapiteau sont fixés (verticalement) deux montants de cuivre, en forme de règle, séparés entre eux par un intervalle égal à l’épaisseur d’une roue ; et sur la même plinthe, entre ces deux montants, se trouve une vis mobile dont les supports sont fixés sur le chapiteau du tube, et qui est ajustée de manière à faire muuvoir cette roue dans un plan vertical. Dans l’intervalle des deux montants, qui s’élèvent à une hauteur de quatre doigts au-dessus du chapiteau, peut s’adapter une règle transversale de quatre coudées de longueur dont la largeur et l’épaisseur sont en rapport avec l’intervalle précédent, et dont la longueur est partagée en deux par le même intervalle.
Sur la surface supérieure de la règle est creusé un canal cylindrique ou quadrangulaire, de dimension convenable pour recevoir un tube de cuivre dont la longueur, prise sur celle de la règle, est d’environ douze doigts. Au tube de cuivre sont fixés à angle droit, par les deux extrémités, deux autres tubes qui semblent n’être qu’une courbure du premier, en formant au-dessus de lui une saillie de deux doigts tout au plus. En outre, le tube de cuivre est enchâssé dans le canal de la règle, auquel on a donné une longueur appropriée à cet objet, de manière que, paraissant faire corps avec elle, il présente ainsi à la vue un aspect plus gracieux. Aux deux points où le grand tube se relève, et de chaque côté, s’emboire un petit tube de verre dont le diamètre lui permet de s’ajuster bout à bout avec le tube de cuivre et dont la hauteur est d’environ douze doigts ; en outre, ces deux petits tubes de verre sont lutés aux deux saillies du tube de cuivre avec de la cire ou tout autre mastic, de sorte que de l’eau versée dans l’un des tubes ne puisse s’échapper d’aucun côté.
Ce n’est pas tout ; sur la règle transversale, là où sont fixés les deux petits tubes de verre, on fixe autour de ceux-ci deux petites enchâssures ou deux petits pilastres creux, dans l’intérieur desquels s’engagent les tubes de verre, de manière à faire corps avec eux. A ces pilastres s’adaptent deux petites lames de cuivre, qui peuvent glisser dans les coulisses, le long de leurs parois, en rasant la surface des tubes de verre, et dont le milieu présente des fentes au travers desquelles ;on peut viser. A ces lames sont fixés, par la partie inférieure, d’autres petits tubes d’un demi-doigt de long, dans lesquels s’engagent des goupilles de cuivre d’une longueur égale à la hauteur des pilastres qui enveloppent les tubes de verre. Ces goupilles pénètrent, par une ouverture, dans la règle qui supporte le tube de cuivre, et s’y implantent au moyen d’un filet de vis qui rencontre son écrou dans l’épaisseur même de la règle. Si donc on fait tourner la tête de ces goupilles qui dépasse dans le bas, on fera, par ce moyen, mouvoir de haut en bas les petites lames qui présentent les fentes dont nous avons parlé. C’est ce qui arrivera nécessairement par l’action de cette extrémité des goupilles qui se trouve engagée dans l’intérieur des petits tubes adhérents aux lames.
Maintenant que nous avons décrit la construction de la dioptre, nous allons parler des poteaux et des disques qui l’accompagnent. On équarrit deux poteaux, longs chacun de dix coudées, larges de cinq doigts et épais de trois. On y pratique sur toute la longueur, et par le milieu de la largeur, une rainure en queue d’aronde, dont la partie étroite soit en dehors. Dans cette rainure s’engage un tenon qui peut y glisser librement sans en sortir. Sur ce tenon est fixé un disque circulaire de dix ou douze doigts de diamètre, que l’on partage, par une droite perpendiculaire à la longueur du poteau, en deux demi-cercles, dont l’un est coloré en blanc et l’autre en noir. Du même tenon part une corde qui, s’enroulant autour d’une poulie située au haut du poteau, se rend à la face postérieure de celui-ci, du côté opposé à celui du disque. Si donc on plante ce poteau dans une position verticale, et que l’on tire la corde par derrière, on fera monter le disque ; si, au contraire, on lâche la corde, le disque descendra en vertu de son poids, surtout si l’on a eu la précaution de clouer, à sa surface postérieure, une plaque de plomb qui aura pour effet de le rendre naturellement plus mobile. Par conséquent, lorsque nous aurons tiré la corde pour élever le disque, nous n’aurons qu’à l’arrêter pour fixer le disque à tel point du poteau que nous voudrons.
En outre, il faut diviser la longueur du poteau, à partir de sa base inférieure, en coudées, palmes et doigts, autant qu’il y en pourra tenir ; puis, par les points de division, tirer des lignes indiquant les parues de la longueur sur celle des faces qui est à droite du disque. Quant à celui-ci, il portera, à sa face postérieure, un index qui, en suivant le diamètre dont on a parlé, ira correspondre aux divisions de l’échelle tracée sur le poteau.
Ce n’est pas tout ; les mêmes poteaux doivent se placer dans une position exactement perpendiculaire au sol, de la manière suivante : du côté opposé à celui où sont tracées les divisions, on implante un piton, long de trois doigts environ, à l’extrémité duquel .se trouve un trou percé de haut en bas, où peut passer un fil portant un poids suspendu. Pareillement, au bas du poteau est implantée une fiche d’une longueur égale à là distance du trou précédent au même poteau ; et, sur la tête de cette fiche, est tracée, par le milieu, une ligne droite verticale. Lorsque le fil à plomb battra contre cette ligne, ce sera une preuve que le poteau est dans une situation rigoureusement verticale.
Parmi les applications décrites par Héron, je citerai les suivantes :
- Mesurer la distance et la différence de hauteur de deux points inaccessibles ;
- percer une montagne suivant une ligne droite qui joigne deux points donnés sur ses flancs ;
- une galerie souterraine quelconque étant donnée, déterminer sur le sol au-dessus, un point tel qu’en y creusant un puits vertical, il aboutisse à un point donné de la galerie ;
- les extrémités d’un port à construire étant données, en tracer le contour sur le terrain suivant une figure semblable à une figure donnée [4] ;
- exhausser un terrain de manière à lui faire prendre la forme d’une surface donnée quelconque ;
- diviser un champ donné de forme quelconque en parties ayant des surfaces données, à l’aide de lignes droites partant toutes d’un point donné [5] ;
- mesurer un champ sans entrer dedans ;
- trouver l’aire d’un triangle en mesurant ses trois côtés [6] ;
- déterminer la distance de deux lieux situés sous des climats différents [7].
Pour mesurer les distances on se servait d’une corde et pour mettre celle-ci hors d’état de s’allonger et de se raccourcir, dit Héron dans ses Automates, "on la tend fortement entre deux lieux, et, après l’avoir ainsi tendue pendant quelque temps, on la tire de nouveau ; après avoir répété cette même manœuvre à plusieurs reprises, on frotte la corde avec un mélange de cire et de résine ; il est préférable, au lieu de la tendre entre deux pieux, de la suspendre verticalement pendant un long temps avec un poids suffisant. »
La dioptre de Héeron servait, nous l’avons vu, pour les nivellements ; mais les anciens employaient également à cet usage d’autres instruments plus simples que Vitruve décrit dans son livre VIII.
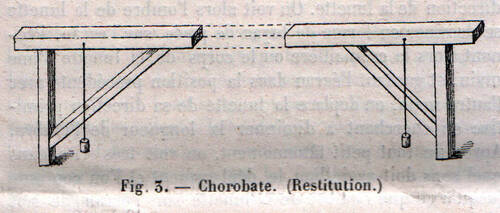
Le chorobate (fig. 3) se compose d’une règle longue d’environ vingt pieds ; aux extrémités de cette règle se trouvent deux pièces ayant la même dimension, qui y sont assemblées à angle droit ; entre la règle et les extrémités de ces deux pièces formant coude, s’étendent deux traverses fixées à l’aide des tenons, sur lesquelles on trace des lignes perpendiculaires (à la règle). Des fils à plomb fixés vers les extrémités de la règle pendent en regard de ces lignes et lorsqu’ils coïncident exactement avec elles, ils montrent que l’instrument est bien de niveau. S’il arrivait que le vent en agitant le fil à plomb l’empêchât de donner une indication certaine, on aurait recours à un canal qui se trouve creusé sur la face supérieure de la règle ; ce canal est long de cinq pieds, large d’un doigt et profond d’un doigt. En y versant de l’eau, on voit si cette eau arrive également aux deux extrémités du canal et par suite si la règle est bien de niveau.
Le bon Vitruve a soin de faire observer ensuite que, malgré la courbure des eaux, qu’a démontrée Archimède, le chorobate n’en est pas moins propre à niveler.
La balance à eau n’était autre chose que notre niveau d’eau actuel.
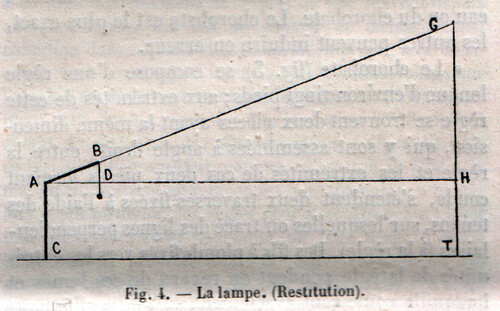
Les anciens faisaient encore usage, pour prendre la hauteur d’un mur ou d’une tour (fig, 4), d’une simple règle AB terminée par un fil à plomb à ses deux extrémités et mobile en A autour d’un axe horizontal fixé à un pied AC que l’on plantait verticalement en terre. On inclinait la règle de façon à viser le sommet G de la hauteur à évaluer. On mesurait les longueurs AD, BD et CT, et par les triangles semblables on avait la hauteur GH ; d’où on tirait GT en ajoutant la hauteur connue du pied.
Cet instrument s’appelait λνχνiα, lampe ; il est décrit dans la Géodésie de Héron le Jeune et dans les Cestes de Jules l’Africain.

